РАСЧЕТ РАЗОМКНУТЫХ ТРЕХФАЗНЫХ СЕТЕЙ С НЕРАВНОМЕРНОЙ НАГРУЗКОЙ ФАЗ
В трехфазных электрических сетях может быть не всегда равномерная нагрузка. В сетях низкого напряжения осветительные потребители и бытовые приборы включают на одну фазу, поэтому нагрузка между фазами бывает неодинаковой, особенно на конечных участках. При использовании смешанной трехфазно-однофазной системы распределения электроэнергии в сетях высокого напряжения также возможна неравномерная нагрузка.
Расчет трехфазных сетей с неравномерной нагрузкой между фазами значительно сложнее, чем сетей с равномерной нагрузкой. В этом случае приходится определять междуфазные потери напряжения между всеми тремя фазами.
Будем считать, что в трехфазной линии сопротивления фазных проводов одинаковые и только сопротивление нулевого провода, если он есть, отличается от фазных.

Пользуясь выведенными формулами, можно найти падение напряжения в любой трехфазной сети с неравномерной нагрузкой.
Соединение однофазных нагрузок в треугольник. Если однофазные нагрузки в трехфазной сети соединить в треугольник (рис. 5.12, а), то в такой схеме нейтраль отсутствует и, следовательно, составляющей тока нулевой последовательности нет.

Подставив в формулу значения синуса и косинуса углов, получим окончательно:

Потерю напряжения между другими фазами определяют по аналогичным уравнениям.
Потерю напряжения в активных сопротивлениях находят по участкам (рис. 5.13), а затем суммируют:
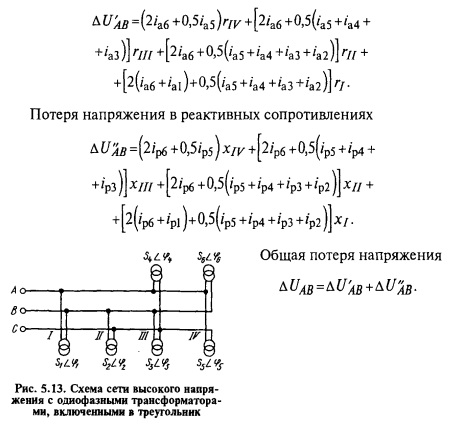
Аналогичным способом находят потери напряжения.
Все выведенные ранее соотношения справедливы для проводов из цветных металлов, у которых сопротивления фазных проводов одинаковы. При использовании стальных проводов такого равенства нет, однако во многих случаях можно пренебрегать этой разницей и вести расчет как для проводов из цветных металлов, считая, что сопротивления всех фазных проводов одинаковы.
Для практических целей большое значение имеет то обстоятельство, что потеря напряжения в сети с неравномерной нагрузкой при правильном исполнении, т.е. при соответствующем распределении нагрузок по фазам, не превышает потери напряжения в ней с такой же нагрузкой сети, но распределенной равномерно. Покажем это в общем виде, допустив, что коэффициент мощности всех нагрузок одинаков.
Пусть есть две одинаковые линии с равной нагрузкой Р. В первом случае она симметрично распределена между фазами, а во втором — неравномерно. Имея в виду, что мощность в обоих случаях одинакова, можем записать:

Таким образом, в трехфазной линии сумма потерь напряжения между фазами при данной передаваемой мощности есть величина постоянная, не зависящая от распределения нагрузок между фазами.
Отсюда можно сделать важный вывод. Если неравномерную нагрузку распределить между фазами так, что все три междуфазные потери напряжения будут равны, то они также будут равны потере напряжения в этой линии при симметричной нагрузке.
Соединение однофазных нагрузок в звезду. При соединении нагрузок в звезду (рис. 5.14, а) линейные токи равны фазным:
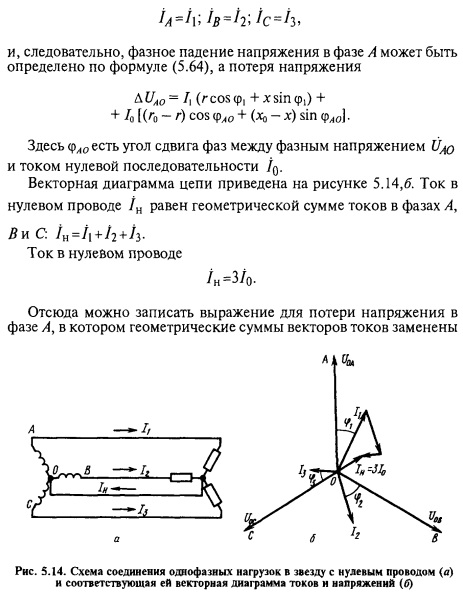
алгебраическими суммами их проекций на напряжение перпендикулярный к нему:


Приведенные ранее формулы применимы также с некоторым допущением и для расчета сетей со стальными проводами.
Общий порядок расчёта сетей с неравномерной нагрузкой, включенной в звезду или в треугольник, заключается в следующем:
1) по возможности распределяют нагрузку между фазами равномерно;
2) определяют сечение проводов сети, считая нагрузку равномерной, описанными ранее способами;
3) определяют фазные или междуфазные потери напряжения по формулам (5.64)...(5.69).
При значительной разнице потерь напряжений в отдельных фазах или между ними нагрузки перераспределяют и рассчитывают заново. Рассмотрим несколько частных случаев.
Четырехпроводная сеть с неравномерной активной нагрузкой фаз. В этом случае, встречающемся в низковольтных сетях с осветительной и бытовой нагрузками, составляющая потери напряжения в реактивных сопротивлениях отсутствует и вся потеря напряжения по фазам составляет
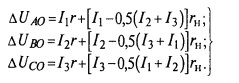
При равномерной нагрузке, второй член в каждом из уравнений становится равным нулю. Тогда уравнения превращаются в обычные выражения для фазной потери напряжения в симметричной трехфазной сети с активной нагрузкой.
Сечения, а следовательно, и сопротивления фазных проводов обычно принимают одинаковыми. Ток нулевого провода, как правило, меньше фазного тока, поэтому сечение нулевого провода в ряде случаев можно брать меньше, чем фазного, но не менее 50 % его значения.
Если на линии несколько нагрузок, то

Трехпроводное ответвление четырехпроводной сети (две фазы и нуль). При трехпроводном ответвлении от четырехпроводной сети (рис. 5.16, а) ток в третьем фазном проводе, очевидно, отсутствует (например, 13 = 0). Потери напряжения в ответвлении определяют по уравнениям (5.70).
 Двухпроводное ответвление от четырехпроводной сети (одна фаза и нуль). Многие потребители в сельских местностях имеют однофазное питание, и к ним подводят два провода — фазный и нулевой (рис. 5.16, б). К таким потребителям относят одноквартирные жилые дома, а также небольшие сооружения общественного и производственного назначения, не имеющие силовой нагрузки. В этом случае фазная потеря напряжения может быть найдена по уравнениям (5.70).
Двухпроводное ответвление от четырехпроводной сети (одна фаза и нуль). Многие потребители в сельских местностях имеют однофазное питание, и к ним подводят два провода — фазный и нулевой (рис. 5.16, б). К таким потребителям относят одноквартирные жилые дома, а также небольшие сооружения общественного и производственного назначения, не имеющие силовой нагрузки. В этом случае фазная потеря напряжения может быть найдена по уравнениям (5.70).

В практических условиях всегда стремятся так распределить однофазные нагрузки по фазам, чтобы в период максимальной нагрузки сети потери напряжения по фазам незначительно отличались одна относительно другой. Расчет значительно упрощается. Кроме того, потеря напряжения в этом случае получается наименьшей.
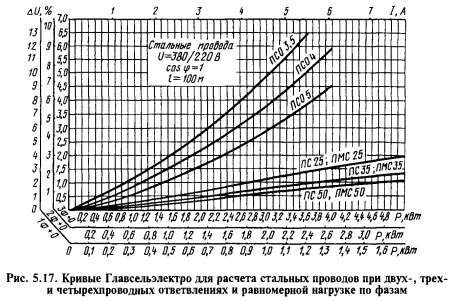
Расчет стальных проводов в четырехпроводной сети сложнее, чем расчет проводов из цветных металлов. Для этой цели были составлены расчетные кривые. Кривые строят для трех-, четырех- и однопроводного ответвлений при условии практически равномерного распределения нагрузок между фазами.
На рисунке 5.17 в качестве примера приведены кривые Главсель-электро для определения потери напряжения в четырехпроводных сетях. Кривые построены для ответвлений: три фазы — нуль, две фазы — нуль и одна фаза — нуль при коэффициенте мощности нагрузки cos ф = 1. Порядок пользования расчетными кривыми такой же, как и в трехпроводных сетях.
Пятипроводная сеть. Для сельской электрификации широко применяют централизованное управление уличным освещением. Для этого прокладывают пятый — фонарный провод, соединенный через рубильник и предохранитель с одной из фаз. Всю нагрузку, включая нагрузку от уличного освещения, следует распределять равномерно между тремя фазами на каждой линии.
Сечение проводов фаз, не имеющих фонарной нагрузки, находят обычным способом. Сечение основного провода фазы, на которую включена фонарная нагрузка, можно взять меньшим, чем сечения других фаз, но его принимают таким же (из удобства монтажа). Сечение фонарного провода определяют, как в трехфазной линии, с равномерной нагрузкой на фазу, равной нагрузке уличного освещения.
И. А. Будзко, Т. Б. Лещинская, В. И. Сукманов, Электроснабжение сельского хозяйства, М., Колос, 2000
