ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ТЕПЛОВЫХ ТРУБ

При расчете параметров тепловых труб приходится также решать задачу выбора оптимальной конструкции, которая наилучшим образом удовлетворяла бы требованиям применения. Вопрос о выборе длины трубы или отдельных ее зон решается исходя из соображений наилучшего сопряжения источника и стока тепла. Далее, возникает вопрос получения максимального теплового потока вдоль осн трубы при выбранных геометрических параметрах корпуса трубы. В простейших случаях расчета параметров тепловой трубы удается записать величину переносимого трубой количества тепла в зависимости от геометрических и теплофизических параметров. Тогда задача оптимизации решается обычным образом — с использованием производной функции теплопереноса по интересующему параметру. Если не удается получить подобного рода аналитическую зависимость, то используют, как правило, численные методы расчета.

Рассмотрим на примерах реализацию этих принципов оптимизации Запишем баланс давления в цилиндрической тепловой трубе с мокрой точкой в конце зоны конденсации без учета влиянии массовых сил:

Выведем соотношение геометрических параметров трубы, прн которых достигается наибольший теплоперенос. Обозначим а — отношение градиента давления в жидкости к градиенту давления в паре

Для тепловых труб возможна такая конструкция фитиля, когда число» канавок или капиллярных трубок остается неизменным, а оптимизация производится за счет изменения их размеров.

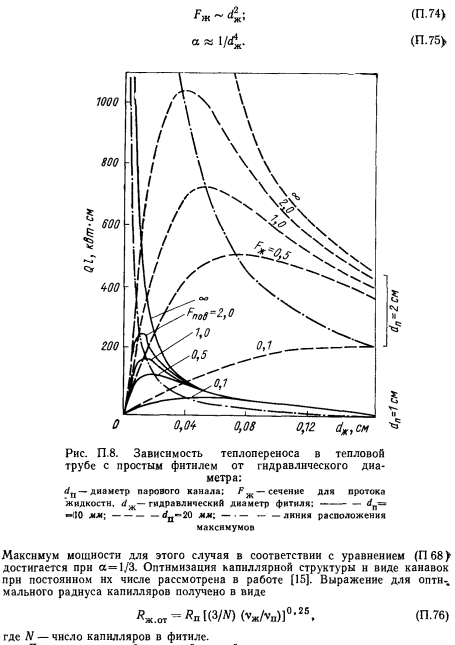
Для тепловых труб с мокрой точкой в произвольном месте зоны конденсации получить аналитическое выражение для оптимального значения геометрических параметров в явном виде весьма затруднительно. Задача может быть успешно решена численными расчетами. Для выяснения оптимального отношения диаметра парового канала к зазору для протока жидкости были проведены расчеты по определению капиллярных ограничений мощности разработанной авторами книги и представленной ниже программе для тепловых труб с составным фитилем в широком диапазоне изменения теплофизических и геометрических параметров. Результаты расчетов для тепловых труб с натриевым теплоносителем представлены в виде графических зависимостей на рис. П.9, П. 10. На примере натриевых тепловых труб влияние таких параметров, как давление пара, размер поры экрана составного фитиля, диаметр и длина трубы, показано на рис. П.9 в виде зависимостей капиллярных ограничений мощности трубы от варьируемого размера зазора для протока жидкости. Мощность трубы отнесена к площади поперечного сечения очерченного внутренним диаметром корпуса тепловой трубы (т. е. сечение включает в себя площадь парового канала и фитиля). Мощность трубы по мере увеличения зазора сначала растет, достигает максимума при определенном зазоре, а затем снижается. Наличие и местоположение максимума кривых на рис. П.9 определяются изменением различных составляющих потерь давления по тракту теплоносителя. При зазоре, меньшем оптимального, капиллярный напор компенсирует главным образом перепад давления в жидкости. По мере увеличения зазора потери давления в жидкости уменьшаются, а максимальная мощность трубы возрастает. Одновременно с увеличением зазора сечение парового канала уменьшается. Это приводит к возрастанию скорости пара и соответственно к увеличению инерционного эффекта и вклада трения в потерн давления в паровом потоке. Увеличение зазора сверх оптимального значения уже не дает заметного выигрыша за счет сокращения потерь давления в жидкости, но при этом возрастают потери на трение в паре из-за уменьшения гидравлического диаметра парового канала. В конечном счете происходит уменьшение переносимой мощности.

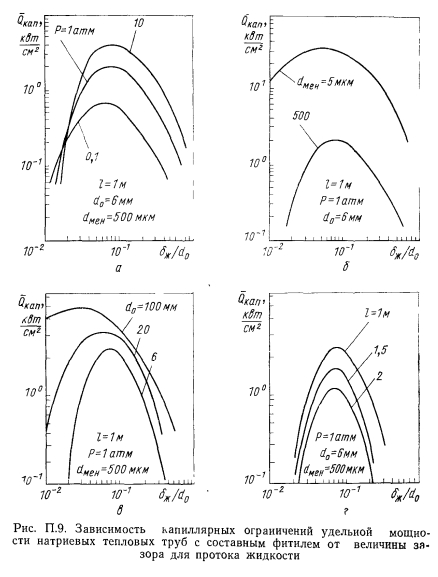
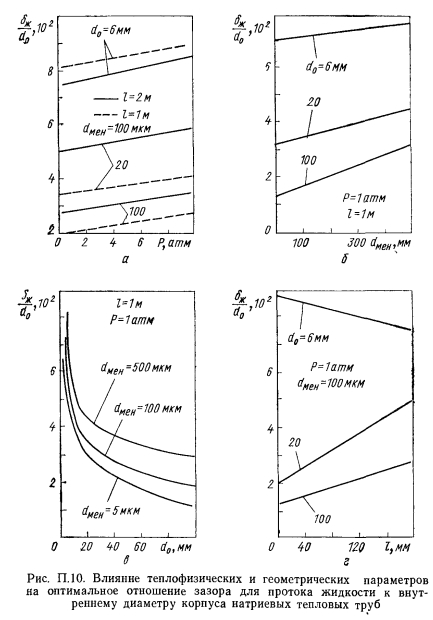
Значение оптимального зазора зависит от уровня максимальной мощности трубы. Для тепловых труб с невысокой мощностью, т. е. для труб с большим размером поры фитиля, кривая зависимости капиллярных ограничений мощности от размера зазора имеет ярко выраженный максимум в узкой области изменения зазора (см. рис. П.9, б, расчеты для труб с 500 мкм). Для тепловых труб большой мощности кривые капиллярных ограничений в области максимума изменяются более плавно. В связи с этим следует говорить не просто об оптимальном отношении размера зазора к внутреннему диаметру трубы, а о диапазоне изменения зазора, в котором мощность трубы будет близка к максимальной. Тенденция к расширению такого диапазона наблюдается и с увеличением диаметра трубы (см. рис. П.9, в). Из всех геометрических параметров длина трубы оказывает наименьшее влияние на оптимальный размер зазора (см. рис. П.9, г). При увеличении рабочей температуры трубы, т е. с ростом давления пара, оптимальный относительный размер зазора увеличивается. Тенденция к увеличению сохраняется независимо от диаметра трубы и радиуса поры фитиля (см. рис. П.10, а). Оптимальный относительный зазор слабо возрастает при увеличении радиуса поры фитиля (см. рис. П.10, б) и заметно уменьшается с ростом диаметра трубы (см. рис. П.10, в). Влияние длины трубы показано на рис. П. 10, г. Из анализа результатов оптимизации следует, что для тепловых труб длиной до 1 м и диаметром парового канала до 20 мм оптимальный зазор можно принимать в пределах от 3 до 7% размера внутреннего диаметра корпуса тепловой трубы. При этом если капиллярная структура имеет крупные поры (до 500 мкм), то необходимо принимать верхнее значение размера зазора Если радиус пор фитиля мал (в пределах от нескольких до десятков микрон), то размер зазора должен быть принят по нижнему пределу. Для тепловых труб большого диаметра (—100 мм) зазор можно принимать в пределах 1,5—3%.

Таким образом, вопрос оптимизации конструкции тепловой трубы в каждом конкретном случае решается аналитически или с применением численных методов расчета в зависимости от условий работы трубы и требований к точности расчета.

Ивановский М. Н., Сорокин В. П., Ягодкин И. В. Физические основы тепловых труб.—М.: Атомиздат, 1978