ПЕРЕПАДЫ ТЕМПЕРАТУРЫ В ТЕПЛОВОЙ ТРУБЕ

Суммарный перепад температуры в тепловой трубе складывается и следующих составляющих: 1) перепадов температуры в стенке трубы в зоне испарения и конденсации; 2) перепадов температуры в фитиле в обеих зонах; 3) перепадов температуры на границе раздела фаз пар — жидкость при испарении и конденсации; 4) перепадов температуры насыщения в паре по длине тепловой трубы.

Перепад температуры в стенке трубы в зонах испарения и конденсации рассчитывается по известным уравнениям теплопроводности: для плоской стенки

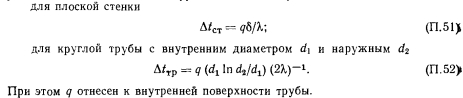
Перепады температуры в фитиле сильно зависят от его конструкции, а в зоне нагрева — и от режима парообразования. Для составного фитиля, имеющего под экраном заполненный теплоносителем зазор, перепад температуры определяется теплопроводностью жидкости и рассчитывается соответствующим формулам теплопроводности с учетом концентрации линий теплового тока вблизи поверхности раздела пар—жидкость в порах экрана» Для простого фитиля в виде пористого тела или многослойной сетки, насыщенных неметаллической жидкостью, перепад температуры рассчитывается по формулам (4 51), (4.52) с использованием эффективной теплопроводности. В теплопереносе от стенки трубы к поверхности испарения участвует как жидкость, так и твердый скелет фитиля. Для фитиля, ие спеченного со стенками трубы и имеющего произвольную пористость, в первом приближении эффективная теплопроводность может быть оценена по формуле

Наибольшее затруднение при расчете ЯЭф простых фитилей из нескольких слоев неспеченных сеток вызывает определение термического сопротивления: в месте контакта проволок сетки фитиля. Для сетчатых фитилей такое сопротивление может быть одним из основных составляющих полного термического сопротивления. Оно определяется степенью прижатия сеток друг к другу в фитиле. Для расчета коэффициента эффективной теплопроводности получена формула [11] которая обобщает результаты опытов, проведенных в широком интервале изменения геометрических параметров (размера поры а, диаметра проволоки dnp и диаметра пятна контакта проволоки dK0HT) Погрешность расчетов ЯЭф по этой формуле не превышает ±12% для фитилей из нескольких слоев сеток, насыщенных теплоносителем, с поджатием в области механических нагрузок, не превышающих предела упругой деформации в следующем диапазоне изменения параметров фитиля:

При отсутствии загрязнений коэффициенты испарения и конденсации для жидких металлов близки к единице [12] Перепады температуры на границе раздела фаз обычно невелики, для неметаллических теплоносителей их можно не учитывать.

Перепады температуры насыщения и давления в паре по длине тепловой трубы. Изменения давления пара и, соответственно, температуры насыщения его по длине трубы определяются переносимой мощностью, а также теплофизическими параметрами теплоносителя и геометрическими параметрами трубы. Наиболее сильное изменение параметров пара имеет место при работе трубы на звуковом пределе переносимой мощности. В этом случае доминирующими факторами, определяющими гидродинамику пара, являются инерционные эффекты Для чисто инерционного режима течения пара (случай коротких труб, когда трением в паре можно пренебречь) изменения давления можно описать в виде зависимости

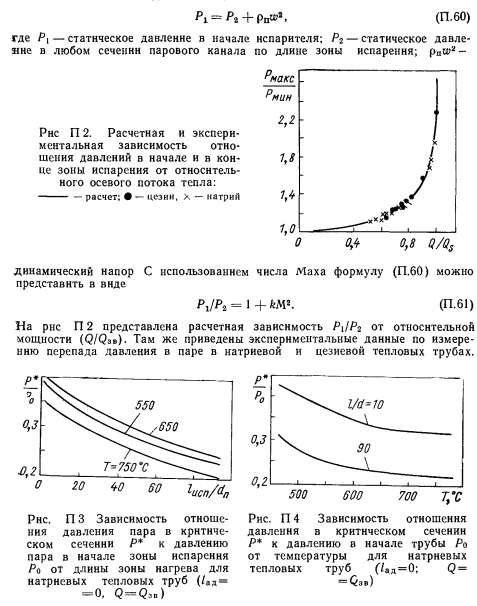
Сопоставление экспериментальных и расчетных данных вполне удовлетворительно для коротких тепловых труб. Для труб в опытах Кемме lacnldn = у2.

Влияние трения проанализировано авторами с использованием модели изоэнтальпийного массового сопла Трение увеличивает перепад давления по длине трубы и приводит к зависимости перепада температуры от длины трубы. На рис. П.З результаты расчетов для натриевых тепловых труб приведены в виде зависимости от длины трубы отношения давления пара в критическом сечении Р к давлению пара Ро в начале зоны испарения. По мере роста длины зоны нагрева перепад давления растет. Зависимость перепада давления в трубе от температуры пара в начале зоны испарения представлена на рис. П.4 для разных длин зоны испарения.

Поведение температуры насыщения пара можно анализировать в соответствии с распределением давления по длине, используя для связи давления и температуры насыщения пара уравнение Клапейрона — Клаузиуса:

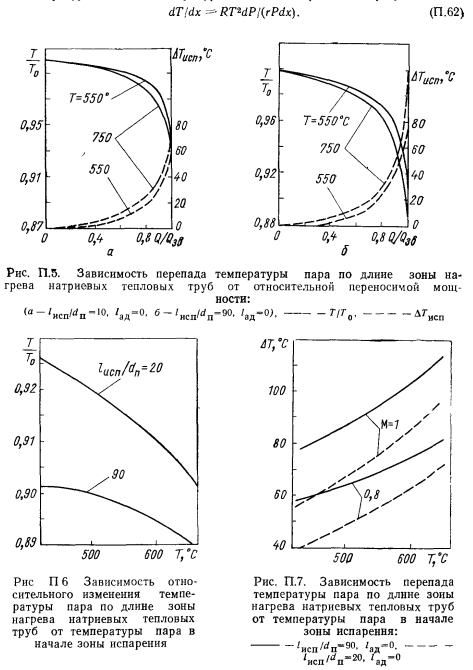
Влияние переносимой мощности на перепад температуры иллюстрируется результатами расчетов, представленными на рис. П.5. По мере роста мощности трубы перепад температуры изменяется нелинейно. Чем ближе мощность трубы к звуковому пределу, тем значительнее рост перепада температуры. Основное увеличение перепада температуры в паре имеет место при увеличении мощности трубы от 80 до 100% значения звукового предела. Так, увеличение мощности трубы от нуля до 80% приводит к падению температуры пара на 2—3% значения То (температуры пара в начале зоны испарения). Увеличение мощности от 80 до 100% Qзв приводит к перепаду температуры до 7—10%. Для достижения изотермичной работы трубы при определенном значении теплопереноса Q следует работать при такой температуре, когда соблюдается условие. Относительный перепад температуры слабо зависит от уровня температуры пара в начале зоны испарения. С ростом давления пара в трубе относительный максимальный перепад температуры Т/Т0 несколько уменьшается (рис П6), а абсолютный перепад температуры АТ увеличивается (рис. П.7). (Расчетные данные на рис П 6 и П.7 представлены в виде зависимости от температуры пара в начале трубы.) Зависимость максимального перепада температуры от давления пара в трубе выражена значительно слабее, чем от переносимой мощности Трение в паре, повышая перепад давления с ростом длины трубы, приводит к увеличению перепада температуры. Это иллюстрируется результатами расчетов авторов, представленных на рис. П.6 и П.7.

Ивановский М. Н., Сорокин В. П., Ягодкин И. В. Физические основы тепловых труб.—М.: Атомиздат, 1978