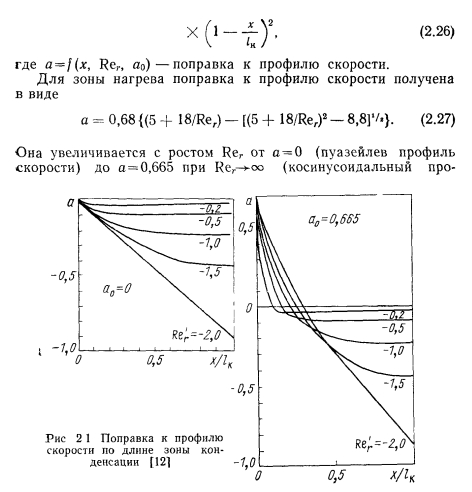
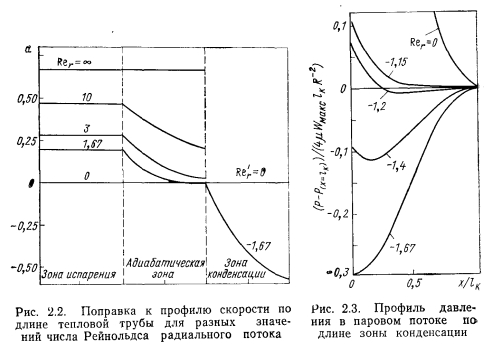
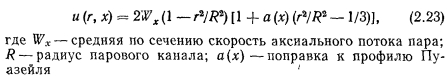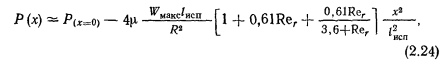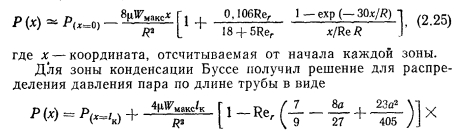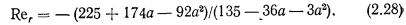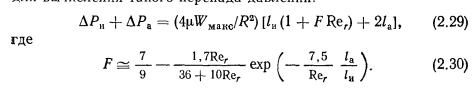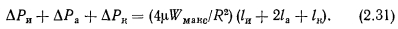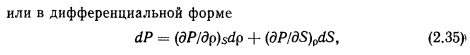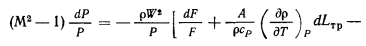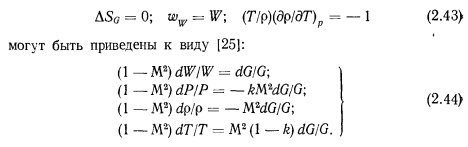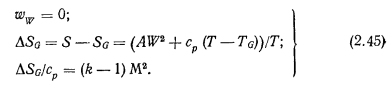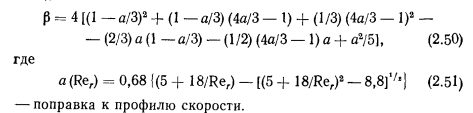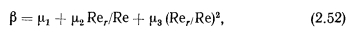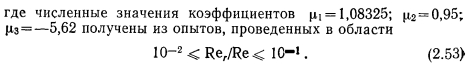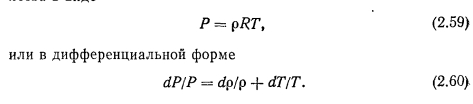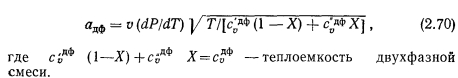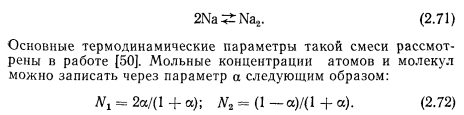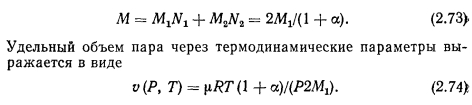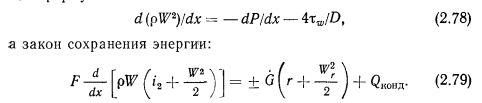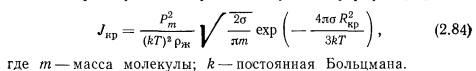ТЕЧЕНИЕ ГАЗА СО ВДУВОМ И ОТСОСОМ МАССЫ. ТЕЧЕНИЕ ПАРА В ТЕПЛОВЫХ ТРУБАХ
Анализ гидродинамики парового потока в тепловых трубах по ряду причин связан со значительными трудностями. Вследствие испарения и конденсации теплоносителя приходится рассматривать поток переменной массы, возникает необходимость учитывать наличие как осевой, так и радиальной составляющей скорости. Вдув при испарении и отсос при конденсации приводят к изменению коэффициента трения на стенке тепловой трубы, число Рейнольдса осевого потока переменно. Изменение давления по ходу потока пара обусловлено не только влиянием трения, но и в значительной мере инерционными эффектами. Разгон пара в зоне испарения создает дополнительный отрицательный градиент давления, а торможение пара в зоне конденсации — положительный градиент давления. При рассмотрении работы трубы в области низких давлений пара, когда мощность трубы близка к звуковому пределу и, соответственно, скорость пара близка к звуковой, необходимо учитывать сжимаемость пара. Если в зоне конденсации достигаются сверхзвуковые скорости, то возможно возникновение скачка уплотнения в этой зоне. Течение пара по длине трубы из-за переменности расхода может иметь зоны с ламинарным, переходным и турбулентным режимами.
Таким образом, гидродинамика пара в тепловых трубах по сравнению с обычно рассматриваемым течением в трубах с непроницаемыми стенками имеет ряд особенностей, которые необходимо в той или иной мере учитывать. Тепловые трубы — своеобразные массовые сопла. Если пренебречь эффектами фазового перехода в паровом потоке (а это иногда допустимо), то гидродинамическая картина в тепловых трубах аналогична той, которая имеет место при течении пара в трубах с пористыми стенками, когда осуществляется вдув или отсос массы газа через стенки.
Задача анализа гидродинамики пара в тепловых трубах — исследование распределения таких параметров потока пара по длине трубы, как давление, температура, скорость, которые необходимы для расчета максимальной мощности трубы или степени неизотермичности поверхности.
В общем случае гидродинамика пара в тепловых трубах может быть описана уравнениями Е[авье—Стокса при соответствующих граничных условиях. При отсутствии внешнего потенциального поля градиент давления пара Р связан со скоростью потока W уравнением
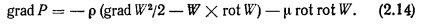
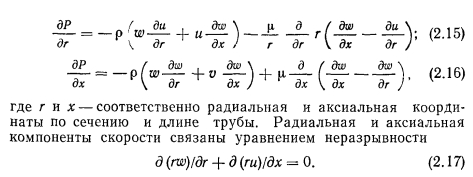
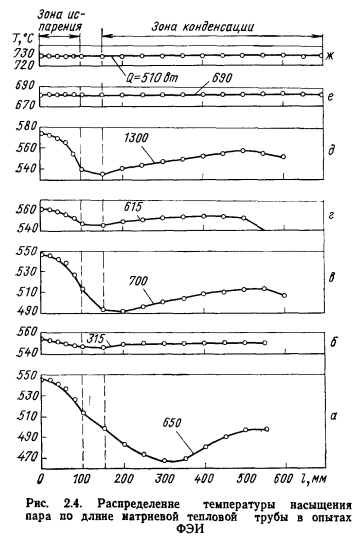
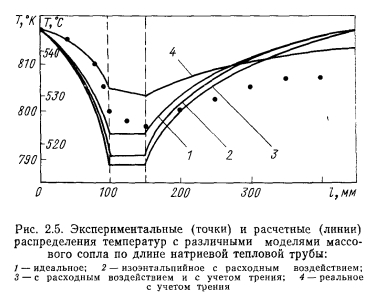
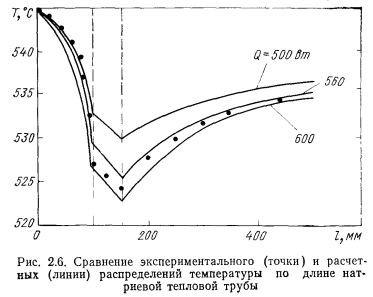
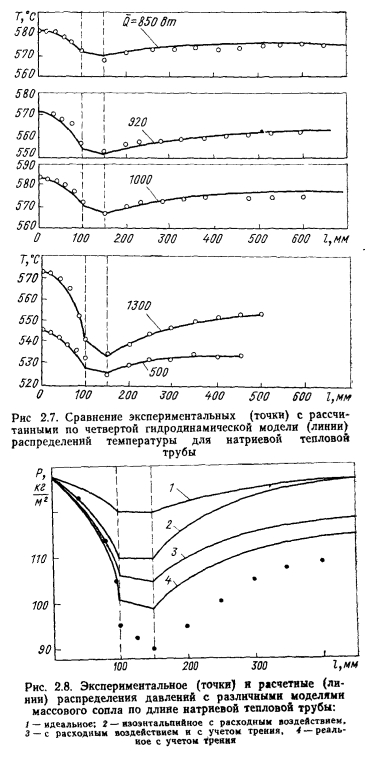
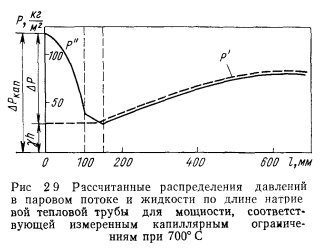
Уравнения Навье—Стокса с граничными условиями, имеющими место в тепловых трубах, решали многие авторы [10— 15]. Юан и Финкелыптейн [10] решали уравнения (2.15) — (2.17) для ламинарного течения жидкости с постоянными по длине трубы вдувом и отсосом массы через пористую стенку цилиндрической трубы. Уравнения Навье—Стокса и неразрывности в предположении линейного соотношения между аксиальной компонентой скорости и осевой координатой с использованием функции потока были приведены к нелинейному дифференциальному уравнению третьего порядка относительно функции профиля скорости в зависимости от осевой координаты х. Входящее в уравнение число Рейнольдса радиального потока определялось следующим образом:

Течение со вдувом и отсосом массы через пористую стенку для Rer
Найт и Мак-Интер [11] теоретически, а Вейгеман и Гуевара [16] экспериментально показали, что в круглой пористой трубе в случае Rer3> 1 давление пара в зоне вдува по ходу потока уменьшается по параболическому закону как функция осевой координаты. Профиль скорости аксиального потока в пористой трубе при больших значениях числа Rer не параболический, а пропорционален cos (я/8) (r/R)2. В зоне отсоса давление растет вследствие торможения потока. При Rer>l осевая скорость практически постоянна по всему сечению трубы и уменьшается до нуля в тонком слое у стенки, т. е. течение имеет вид пограничного слоя. Решение уравнений Навье—Стокса для ламинарного течения несжимаемой жидкости в пористой трубе получено методом возмущений путем разложения в ряд по числам 1/Rer в области значений l/Re,->-0, т. е. при Rer>l. Для градиента давления в работе [11] получена формула
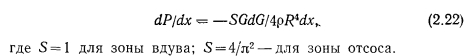
Результаты исследований, полученные в работах [10, 11, 161, были использованы Коттером [17] при создании первой расчетной модели для тепловых труб. Расчетная модель Коттера для гидродинамики пара в тепловых трубах предполагала наличие перестройки профиля скорости на границе между зонами вдува и отсоса (испарения и конденсации). При этом допускалось, что перестройка происходит при незначительных потерях давления осевого потока. Такое предположение выполняется удовлетворительно в том случае, когда профиль скорости осевого потока мало отличается от профиля Пуазейля (т. е. при Rer Дальнейший анализ гидродинамики пара в тепловых трубах, основанный на использовании уравнений Навье—Стокса, был сделан Буссе [12]. Уравнения Навье — Стокса и неразрывности с соответствующими граничными условиями записаны для ламинарного несжимаемого потока пара в длинной цилиндрической тепловой трубе, имеющей зоны: испарения, адиабатическую и конденсации, с постоянным по длине подводом и отводом тепла. При этом принималось, что длина каждой зоны намного больше диаметра парового канала. Для решения уравнений Навье—Стокса профиль аксиальной скорости был аппроксимирован полиномом четвертой степени, записанным в виде В зоне нагрева при Rer->0 решение уравнения для профиля скорости дает профиль близкий к пуазейлеву. При Rer--oo профиль скорости приближенно можно описать косинусоидальной функцией. В адиабатической зоне тепловой трубы профиль скорости близок к пуазейлеву. В зоне конденсации аппроксимация профиля аксиальной скорости полиномом 4-й степени радиуса пригодна лишь при (Rer) < 1. Интегрирование уравнений Навье—Стокса при соответствующих граничных условиях в зоне нагрева дает параболическое распределение профиля давления пара по длине трубы. Это распределение с погрешностью менее 1% было аппроксимировано приближенной формулой В адиабатической зоне тепловой трубы распределение давления парового потока с погрешностью до 4% аппроксимировано Буссе следующей зависимостью: Распределение давления пара по длине зоны конденсации в отличие от зоны испарения, где профиль давления параболический, существенно зависит от числа Рейнольдса радиального потока, а также от профиля скорости пара на входе в конденсаторную зону. На рис. 2.3 представлен ход давления пара по длине зоны конденсации для некоторых значений Re,, и — т. е. в предположении, что адиабатическая зона достаточно длинна, чтобы в конце ее профиль скорости практически не отличался от параболы Пуазейля. Анализ хода давления пара на рис. 2.3 показывает, что до определенного значения Rer (около 1,15) минимум давления пара располагается в конце зоны конденсации. При увеличении Rer минимум давления начинает смещаться к началу зоны охлаждения, а местоположение минимума давления пара определяется из соотношения Местоположение минимума давления в основном зависит от значений Rer и а0, т. е. от интенсивности конденсации и профиля скорости на входе в конденсаторную зону. Число Рейнольдса, при котором минимум давления пара находится в начале зоны отвода тепла, уменьшается монотонно от —1,7 до 2,7 при увеличении а0 от 0 до 0,665. Рост давления пара по длине зоны конденсации может приводить к смещению мокрой точки от конца к началу зоны, и тогда падение давления в тепловой трубе рассчитывают только по двум зонам — испарения и адиабатической. Буссе приводит следующую формулу для вычисления такого перепада давлений: Поправочный фактор F учитывает инерционный эффект и изменение падения давления вследствие трения при отклонении профиля скорости от профиля течения Пуазейля и изменяется в пределах от 0,6 до 0,8, возрастая с увеличением Rer. Следует обратить внимание на то, что если минимум давления приходится на конец зоны конденсации, то полное падение давления пара на длине тепловой трубы определяется только потерями на трение, т. е. Инерционные эффекты на испарительной и конденсаторной частях тепловой трубы взаимно исключают друг друга. Итак, для простейшего случая цилиндрической трубы и постоянных по длине испарительной и конденсаторной зон удельных тепловых потоков работы Юана и Финкелыптейна [10], Найта и Мак-Интера [11], Коттера [17] и Буссе [12] позволяют «описать гидродинамику несжимаемого парового потока при ламинарном течении и получить аналитические зависимости для определения профиля давления пара по длине трубы. Расчетные соотношения (2.24) — (2.27) можно использовать лишь в том случае, когда перепады давления пара по длине трубы невелики и, следовательно, пар допустимо считать несжимаемым. При существенном изменении давления пара в трубе модели несжимаемого потока пара могут давать значительные погрешности, приводить к физически не оправданным результатам. Например, по модели Коттера максимальное значение восстановления давления пара в зоне конденсации составляет 4/я2«40,5% падения давления пара в зоне испарения и не зависит от переносимой мощности. Наши опыты, описанные ниже, а также опыты Кемме [18] не подтверждают этого. Так, в работе [18] указывается, что в опытах восстановление давления пара по длине зоны конденсации при Rer>10 достигало 60% перепада давления в зоне испарения. Изменение степени восстановления при учете сжимаемости подтверждается и расчетными работами. Так, расчеты изменения давления по длине натриевой трубы с учетом сжимаемости парового потока показали [19], что степень восстановления давления пара в зоне конденсации зависит от передаваемой по трубе мощности и уровня рабочей температуры. По мере возрастания мощности трубы при неизменной геометрии (Rer растет) перепад давления по зоне испарения увеличивается, а в зоне конденсации эффект восстановления возрастает из-за торможения парового потока и достигает 90% перепада давления пара по зоне нагрева. При неизменной мощности трубы степень восстановления растет по мере понижения температуры и, соответственно, давления пара. Учет влияния сжимаемости парового потока в уравнениях Навье — Стокса, представляющий значительную трудность, проводят численными методами с разработкой сложных программ и с большими затратами машинного времени. Одномерные модели гидродинамики парового потока. Значительную информацию о процессах гидродинамики парового потока в тепловых трубах при существенном упрощении подхода к задаче можно получить на основании рассмотрения одномерных моделей парового потока. Ценность одномерного подхода состоит в том, что помимо сжимаемости при его использовании можно приближенно учесть такие факторы, как изменение проходного сечения тепловой трубы, а также переменность удельных тепловых потоков в зоне нагрева и конденсации. Одномерный подход при решении задачи о течении пара в цилиндрических тепловых трубах с учетом сжимаемости был использован в работах Леви [20, 21]. Исследования процессов гидродинамики пара на основании одномерных моделей параллельно с Леви проводили и авторы данной книги. Рассмотрим четыре одномерные модели гидродинамики пара в тепловых трубах. Движущийся по каналу пар может находиться под влиянием различных воздействий, приводящих к изменению скорости движения, давления, температуры. Для определения изменения параметров пара по длине трубы можно использовать уравнения неразрывности и энергии для потока переменной массы в канале произвольного сечения (обобщенное уравнение Бернулли) : Дифференциал энтропии выразим на основе второго начала термодинамики для потока переменной массы: Уравнение скорости движения (2.38) дополним выражениями для основных термодинамических параметров: давления, плотности, температуры. Выражение для давления в паровом потоке получим умножением равенства (2.33) на величину (М2—1) и заменой произведения (М2—1 )dW/W его выражением из (2.38). Преобразуя полученное соотношение относительно величины дифференциала давления, получаем Температура пара в предположении, что объемная конденсация в потоке пара отсутствует, может быть представлена в виде функции двух независимых переменных: Совокупность уравнений (2.38), (2.39), (2.42) характеризует состояние потока пара в трубе при наличии таких воздействий, как изменение поперечного сечения канала — dF/F (геометрическое воздействие), изменение расхода массы dG/G (расходное воздействие), изменение dLTp (механическое воздействие)г а также внешний подвод или отвод тепла dQa (тепловое воздействие). Тепловую трубу, таким образом, можно рассматривать как сопло с различными воздействиями. Скорость пара на входе в конденсаторную зону может достигать скорости звука,, что приводит к звуковому ограничению передаваемой мощности. В зоне конденсации воздействия меняют свой знак и в. соответствии с общим законом об обращении воздействий, который был впервые сформулирован JI. А. Вулисом [22—25], паровой поток может разгоняться до сверхзвуковых скоростей. При работе цилиндрической тепловой трубы с постоянным по длине сечением (dF = 0) в первую очередь следует учитывать такие воздействия, как расходное и трение. Основной вклад в изменение параметров пара при этом дает, как правило, расходное воздействие. Оно может быть различным. Наиболее простой случай — идеальное расходное сопло, которое характеризуется изоэнтропическим энергетически изолированным движением пара (первая одномерная модель гидродинамики парового потока). Уравнения (2.38), (2.39), (2.42) с учетом соотношений для изоэитропического течения Практически же вдуваемый пар может иметь параметры, не совпадающие с параметрами основного потока. В частности, может иметь место различие векторов скорости основного и вдуваемого потоков. При вдуве пара перпендикулярно к осевому потоку имеем: Прирост энтропии A?G пропорционален сумме абсолютных величин разностей кинетической энергии и энтальпии в основном и вдуваемом потоках. Исходная система уравнений с учетом этих соотношений для реального массового сопла без учета трения имеет вид (вторая одномерная модель гидродинамики парового потока): Рассмотренные выше одномерные гидродинамические модели течения пара в тепловой трубе, основанные на представлении ее в виде массового сопла с добавлением воздействия трения, не дают возможности учесть влияние перестройки профиля скорости потока пара от сечения к сечению на параметры парового потока, а также особенности фазового перехода в зонах испарения и конденсации Авторы данной книги наряду с изложенными выше моделями рассмотрели четвертую модель, основанную на использовании уравнения энергии с учетом трения и перестройки профиля скорости в паровом потоке. Уравнение энергии потока переменной массы получено в работах И. С Коченова и О. Ю. Новосельского [26, 27] (член, учитывающий трение, введен авторами). Это уравнение имеет вид Уравнение (2.49) получено в предположении, что вдуваемый поток направлен перпендикулярно к основному потоку, т. е. проекция скорости вдуваемого потока на направление основного потока равна нулю. Использование такого выражения при анализе гидродинамики парового потока в тепловых трубах весьма результативно, так как позволяет использовать обширный экспериментальный и теоретический материал, полученный при решении задач, связанных со вдувом и отсосом газа в каналах с пористыми стенками. Основную трудность при решении гидродинамической задачи с использованием этого уравнения представляет необходимость корректного представления величин р и , которые являются функциями Re и Re,. Для нахождения величин р и необходимо привлечь дополнительные соотношения, полученные экспериментально или теоретически. Помимо уравнения (2 49) в рассматриваемой четвертой модели гидродинамики пара в тепловой трубе использовались, уравнения: неразрывности, состояния парового потока (уравнение Клапейрона — Менделеева), а также — при нахождении температуры насыщения пара — уравнение Клапейрона — Клаузиуса. Значение коэффициента потока импульса р, определяющее отношение истинного потока импульса по всему сечению трубы к потоку импульса, вычисленному по средней скорости одномерного потока, рассчитывали посредством интегрирования профиля скорости При ламинарном течении пара в зоне нагрева использовалась аналитическая зависимость для профиля скорости, полученная Буссе [12]. Для турбулентного потока интегрирование велось для косинусоидального профиля скорости, наличие которою подтверждено экспериментально в работе [1(3] в широком диапазоне изменения Re осевого потока — вплоть до Re«105. В работе [28] на основе результатов Буссе [12] приведена аналитическая зависимость для расчета величины р при ламинарном течении пара с погрешностью до -2 о/о Для турбулентного режима течения пара в зоне испарения в работе [28] рекомендована следующая зависимость, полученная путем аппроксимации экспериментальных данных работ [29-31] Коэффициент потока импульса р для зоны конденсации без значительной погрешности может быть принят равным единице. Экспериментально показано [30, 31], что при lK/dn> 10 значение р при турбулентном течении стремится к автомодельному, равному 1,018. (2.54) Коэффициент трения при вдуве и отсосе — функция не только локального критерия Re, но и Rer. При вдуве локальное значение коэффициента трения уменьшается, а при отсосе увеличивается по сравнению со значением его в трубе с непроницаемой стенкой при одинаковых Re. При практических расчетах перепада давления в паре для коротких тепловых труб с интенсивным теплопереносом коэффициент трения может приниматься в первом приближении зависящим только от Re. Такое приближение не приведет к значительным погрешностям в расчетах, так как вклад трения в указанном случае относительно невелик. Результаты исследований коэффициента трения при вдуве и отсосе применительно к тепловым трубам наиболее полно представлены в работе [28]. Для ламинарного режима течения пара в зоне испарения на основе результатов работы Буссе [12] рекомендована следующая формула: Выше приведены лишь некоторые из полученных теоретически и экспериментально соотношений, определяющих гидродинамику потока жидкости в каналах со вдувом и отсосом массы, с испарением и конденсацией. Дополнительные сведения по рассматриваемому вопросу читатель может получить в работах [32—39]. Экспериментальное исследование распределения температуры по длине в натриевых тепловых трубах. Экспериментальные исследования распределения температуры по длине тепловых труб проводятся, как правило, посредством измерения температуры стенки с помощью пирометра, термовизора или термопар, заделанных на наружной поверхности корпуса тепловой трубы [40—42]. Однако такой метод измерения температуры из-за необходимости учета перепадов температуры в стенке и фитиле часто дает значительные погрешности и не позволяет с достаточной точностью сравнить экспериментально полученное распределение температуры с рассчитанным. Размещение термопар непосредственно в паровом потоке дает значительно большие возможности. В первых экспериментах с натриевыми тепловыми трубами авторы книги исследовали распределение температуры пара по длине трубы, используя неподвижные термопары, размещенные в паровом потоке в тонкостенных гильзах [43]. Затем методика измерения распределения температуры по длине трубы была усовершенствована — использована подвижная микротермопара, также расположенная непосредственно в паровом канале. При этом в зоне возможного перегрева термопары вследствие аэродинамического нагрева были приняты конструкционные меры, чтобы реализовать идею мокрого термометра. Термопара была снабжена специальным капиллярным устройством, которое обеспечивало смачивание ее конденсатом. Конструкция тепловой трубы в целом была выбрана таким образом, чтобы наиболее важные конструкционные параметры соответствовали требованиям проверки расчетной модели и сохранялись неизменными в процессе проведения экспериментов. Тепловая труба была снабжена составным фитилем экранного типа с кольцевым зазором для протока жидкости. Основные геометрические размеры трубы следующие: Детальное описание конструкционных особенностей этой натриевой тепловой трубы будет дано в книге «Технологические основы тепловых труб». Опыты проводились при положении трубы, близком к горизонтальному (с очень малым наклоном вниз конденсаторной части). Использование подвижной термопары позволило детально измерять распределение температуры насыщения пара по длине трубы. На рис. 2.4 представлены распределения температур для некоторых режимов работы трубы в стационарных условиях при дозвуковых скоростях течения пара. Давление пара (соответственно и температура насыщения) в зоне испарения по ходу парового потока падает из-за наличия трения, а также разгона потока вследствие притока массы пара. В зоне конденсации отсос массы приводит к торможению потока, т. е. к повышению давления, а трение понижает давление в потоке пара В зависимости от соотношения этих эффектов (трения и инерционною эффекта) характер изменения давления может быть различным. Представленные на рис. 2.4 измеренные распределения температур указывают на то, что степень неизотермичности по длине трубы в значительной мере определяется не только переносимой мощностью, но и уровнем температуры. В целом, для всех представленных распределений температур характерна высокая степень восстановления давления пара в зоне конденсации Соотношение между инерционным вкладом и трением, т е. степень восстановления давления, зависит от переносимой мощности, относительной длины зоны конденсации и давления пара Первые два параметра определяют значение Rer Чем ниже давление, выше мощность и короче зона теплоотвода, тем больше вклад инерционного эффекта В коротких высокотемпературных тепловых трубах при сравнительно высокой переносимой мощности преобладающим, как правило, является инерционный вклад В очень длинных тепловых трубах падение давления вследствие наличия трения в зоне конденсации может быть сравнимым или же преобладающим над величиной инерционного вклада. Распределения температуры, представленные на рис 2.4, характерны для относительно коротких тепловых труб Отметим, что при работе трубы с теплопереносом Q = 1300 и 615 вт (режимы г, д) минимум давления пара приходится на начало зоны конденсации — инерционный вклад преобладает над трением. При мощности Q = 700 вт (режим в), но при более низком давлении пара в трубе минимум несколько смещен по отношению к началу зоны конденсации, т. е в начале этой зоны трение дает несколько больший вклад в изменение давления, чем инерционный эффект. На рис. 2 4, а представлено поле температуры при мощности трубы Q — = 650 вт. В таком режиме минимум давления уже значительно смещен от начала зоны конденсации к ее середине, т. е. в начале зоны теплоотвода трение значительно преобладает над инерционным эффектом. Там же приведено распределение температур по длине трубы при мощности Q = 315 вт. Хотя давление пара и низкое, при такой невысокой мощности поле температуры близко к изотермичному. По мере повышения давления уменьшается градиент йТ'/dP", плотность пара растет, а скорость пара при сохранении переносимой мощности сильно уменьшается. Поэтому инерционный эффект и трение не приводят к значительным перепадам температуры, которые наблюдаются при низком давлении пара. Тепловые трубы при повышенных давлениях пара начинают работать в характерном для них изотермическом режиме. На рис. 2.4, е, ж приведены примеры распределения температуры по длине тепловой трубы„ работающей в изотермических режимах при различной переносимой мощности. Сравнение экспериментальных результатов с расчетными- Результаты расчетов распределения температуры пара по длине трубы по четырем рассмотренным выше одномерным гидродинамическим моделям сопоставлены на рис. 2.5 с экспериментальными данными, полученными авторами на натриевой тепловой трубе. Из приведенных результатов следует, что первые три модели гидродинамики пара, основанные на представлении температуры пара в виде функции независимых переменных плотности и давления, дают занижение температуры пара в конце зоны испарения и неверный ход кривых в адиабатической зоне (кривые 1—3 на рис. 2.5). В конденсаторной зоне эти модели даже с учетом трения дают почти полное восстановление температуры. В действительности, в тепловых трубах уровень температуры из-за влияния трения в конденсаторной зоне становится постоянным и может даже понижаться. Четвертая модель, в которой рассчитывается температура насыщения пара с использованием уравнения Клапейрона— Клаузиуса и градиента давления пара, учитывающего разгон и трение в потоке, дает качественно правильное описание распределения температуры по длине трубы и в целом наилучшее количественное согласование с экспериментальными данными. В экспериментах мощность трубы измерялась с погрешностью до 6—10%. На рис. 2.6 дано сравнение экспериментально измеренных температур с результатами расчетов для трех различных значений мощности — измеренной и с отклонениями от нее на ±10%. На рис. 2.7 представлены результаты сопоставления ряда измеренных и рассчитанных по четвертой модели распределений температуры для некоторых режимов работы трубы. Из сравнения следует, что экспериментальные и рассчитанные распределения температуры при измеренных значениях мощности трубы довольно хорошо согласуются. Некоторое расхождение экспериментальных распределений температур с рассчитанными, занижение расчетных температур в зоне испарения и завышение их в зоне конденсации объясняются тем, что коэффициент трения рассчитывался приближенно — без учета вдува и отсоса. По измеренному распределению температур (см. рис. 2.5) определено распределение давлений в паре по длине трубы (рис. 2.8) в предположении, что в каждом сечении трубы устанавливается давление насыщения в соответствии с измеренной температурой. Это распределение давлений сопоставлено с рассчитанным распределением давления по четырем одномерным моделям. Из представленных результатов расчета распределения давлений следует, что значение и характер изменения давления зависят от степени учета различных факторов, влияющих на параметры потока. В идеальном массовом сопле (первая модель — кривая 1 на рис. 2.8), в котором на поток пара воздействуют только вдув и отсос массы с теми же параметрами что и в основном потоке, без изменения энтропии, изменение давления по длине трубы наименьшее. В изоэнтальпийном массовом сопле (вторая модель — кривая 2), в котором втекающая за счет испарения и вытекающая за счет конденсации масса пара имеет перпендикулярную к основному потоку скорость, энтропия в потоке изменяется, а падение пара по зоне испарения тепловой трубы увеличивается по сравнению с первой моделью. Учет трения в изоэнтальпийном массовом сопле (третья модель — кривая 3) приводит к дальнейшему увеличению изменения давления пара по длине трубы. Учет влияния перестройки потока под воздействием изменяющейся по длине массы пара за счет фактора р в четвертой модели (кривая 4) приводит к дополнительному изменению давления пара в зоне испарения, т. е. в зоне изменения р. Так как в зоне конденсации принималось, что р«1, кривые изменения давления пара по этой зоне для двух последних моделей (кривые 3, 4) идут эквидистантно. В моделях гидродинамики пара без учета влияния трения на характеристики потока в адиабатической зоне давление пара неизменно, а в зоне конденсации имеет место» полное восстановление его за счет торможения до значения давления пара на торце трубы в зоне нагрева (кривые 1, 2). Учет трения приводит к неполному восстановлению давления- пара по длине зоны конденсации (кривые 3, 4). Сопоставление рассчитанных распределений давления пара по длине трубы по четырем одномерным моделям гидродинамики с распределением давления, соответствующим измеренной по длине температуре пара, дает наилучшее согласование с расчетом по- четвертой модели. Для данной анализируемой натриевой тепловой трубы при мощности, соответствующей измеренному капиллярному ограничению при температуре около 700° С, по четвертой модели, рассчитаны распределения давлений в паре и жидкости по длине трубы. На рис. 2.9 представлены результаты расчета. В соответствии с этими результатами суммарные потери давления в трубе с учетом местоположения мокрой точки и влияния гравитации на работу трубы с небольшой погрешностью соответствуют движущему капиллярному перепаду давлений, создаваемому порами экрана составного фитиля. Представленные выше результаты показывают, что разработанная авторами четвертая расчетная гидродинамическая модель, дает приемлемое согласование расчетных распределений температур и давлений по длине трубы с полученными экспериментально. Она может служить основой для анализа гидродинамических процессов в паровом потоке, а также для расчета параметров трубы в дозвуковых режимах течения пара. Модели состояния пара. На расчетные характеристики тепловых труб оказывают влияние не только выбор модели массового сопла, учет трения и других факторов в паровом потоке, но и принимаемая модель при описании уравнения состояния пара. Влияние принимаемых моделей уравнения состояния пара обсуждается в ряде работ [20, 21, 28, 42—45]. В этих работах рассмотрены различные модели состояния парового потока, учитывающие протекание тех или иных процессов в паре по мере его течения вдоль трубы. Неоднозначность моделей связана с тем, что в зоне нагрева образуется пар в условиях насыщения, а затем по ходу потока, давление и другие параметры пара (например, температура, плотность) понижаются. В качестве первой наипростейшей модели для описания состояния пара принимается модель идеального газа с использованием уравнения Клапейрона—Менделеева, которая дает хорошую качественную картину поведения сжимаемого потока.Однако она не учитывает возможного появления жидкой фазы в шаровом потоке вследствие объемной конденсации. Вторая модель— модель равновесного двухфазного потока — учитывает этот фактор. Модель используется в предположении, что пар представляет собой смесь идеального газа и жидкой фазы, находящихся в равновесии [20, 28]. Следует отметить, что образование жидкой фазы в паровом потоке, в особенности для щелочно-металлических теплоносителей, весьма маловероятно вследствие действия двух факторов. Во-первых, циркуляция теплоносителя в тепловой трубе представляет собой процесс непрерывной дистилляции жидкости, и в паровом потоке, как правило, отсутствуют центры конденсации. Это в особенности справедливо для тепловых труб, конструкция фитиля которых: затрудняет попадание капелек жидкости в паровой поток. Например, в тепловых трубах с составным фитилем при использовании мелкопористого ячеистого экрана попадание капелек жидкости в паровой канал практически исключается по крайней мере по длине зон испарения и адиабатической. В этих зонах поверхность жидкости в фитиле имеет, как правило, вогнутый мениск и нет рециркуляции теплоносителя. Во-вторых,, на этих длинах трубы степень пересыщения, необходимая для начала спонтанной конденсации в паровом потоке, трудно достижима. В парах щелочных металлов в условиях изменения температуры по длине трубы возможно протекание химической реакции— димеризации. Возможность влияния этой реакции на характеристики тепловой трубы отмечена авторами работы [46} при экспериментальном изучении предельных характеристик натриевых тепловых труб в области давлений пара, где достижимы звуковые ограничения. Поэтому в качестве третьей модели состояния пара в работе [45] рассмотрена так называемая соединительная модель. В этой модели пар описывается как двухкомпонентная смесь (мономер и димер) идеальных газов, которая находится в локальном химическом равновесии, но эта смесь «заморожена» по отношению к фазовым переходам, т. е. предполагается отсутствие конденсации в паровом потоке. Была проанализирована [27] также четвертая модель описания состояния пара, в которую включены кинетика протекания реакций диссоциации: рекомбинации, процесс зародышеобразования капелек жидкости, а также процесс роста капель. Рассмотрим эти модели состояния пара. Модель идеального газа. Для описания состояния идеального газа используется уравнение Клапейрона—Менделеева в виде Совокупности уравнений для описания параметров пара по длине тепловой трубы для различных массовых сопл с использованием описания состояния пара по модели идеального газа получены выше. Модель равновесного двухфазного потока. Основные соотношения в двухфазной области для описания состояния парового потока, замороженного по отношению к химическим превращениям, запишем через параметры насыщенного пара и насыщенной жидкости. Будем считать, что пар представляет собой равновесную двухфазную смесь. Тогда имеем Скорость звука в равновесной двухфазной смеси с учетом • сухости пара можно определить как [47] Используя формулы (2.37), (2.56) — (2.70), можно получить выражения для градиента давления, температуры, сухости, плотности и размерной и безразмерной скорости пара. Такие выражения без учета трения в потоке и влияния перестройки потока пара на его параметры получены Леви [20], а позднее с учетом трения и перестройки профиля скорости по длине трубы — в работе [28]. Соединительная модель и химически реагирующая смесь атомарной и молекулярной компонент двухфазного потока. Так как модель химически реагирующей смеси атомарной и молекулярной компонент двухфазного потока включает в себя и соединительную модель, то рассмотрим их совместно на примере гидродинамики парового потока в тепловой трубе с натриевым теплоносителем. Впервые о существовании в парах щелочных металлов двухатомных молекул стало известно в 30-е годы [48, 49]. В настоящее время общепризнано, что пары щелочных металлов при давлениях, далеких от критических, являются частично димеризованными, т. е. содержат не только атомы, но и многоатомные молекулы [50]. Состояние равновесия при заданных температуре и давлении характеризуется определенными концентрациями атомов и молекул. Эти концентрации определяются константой равновесия, соответствующей реакции диссоциации — рекомбинации. Доля каждой компоненты в паре определяется через параметр а, называемый степенью диссоциации. По определению, величина а является долей числа молекул, продиссоциировавших в данном равновесном состоянии пара с параметрами Р и Т. Таким образом, пары металлов следует рассматривать как химически реагирующую смесь атомарной и молекулярной компонент. В натриевых тепловых трубах по ходу парового потока возможно протекание реакции диссоциации — рекомбинации: Если представить эту смесь в виде идеального газа, то относительная молекулярная масса пара будет определяться выражением Формулы для расчета мольных и удельных значений энтальпии,, энтропии и теплоемкости пара приведены также в работе [50]. Вследствие непрерывного притока массы пара и разгона потока происходит понижение температуры по ходу потока вдоль зоны нагрева. А это, в свою очередь, может привести к пересыщению пара в потоке При определенной степени пересыщения пара возможно спонтанное зародышеобразование — появление и рост капель. Степень пересыщения зависит,, в свою очередь, от интенсивности реакции диссоциации — рекомбинации. Поэтому необходимо рассматривать одновременно кинетику химического процесса зародышеобразования. Исследованию влияния реакции диссоциации — рекомбинации пара, процесса зародышеобразования и роста капель жидкости на поведение пересыщенною пара, движущегося в паровом тракте натриевой тепловой трубы, посвящена работа [21]. Для цилиндрической тепловой трубы в предположении стационарности и одномерности парового потока, представляющего собой гомогенную смесь одно- и двухатомных паров, а также капель жидкости, закон сохранения для всей массы записывается в виде Закон сохранения количества движения выражен следую тцей формулой: Знак « + » относится к параметрам вдуваемой массы в зоне испарения; знак «—» — к параметрам отсасываемого пара в зоне конденсации; ir — энтальпия подводимого или отводимого пара. Плотность влажного пара, состоящего предположительно из идеального газа (одно- и двухатомные молекулы пара) и капелек жидкости, выражена следующим образом: В паровом потоке тепловой трубы должен происходить процесс гомогенной конденсации переохлажденного пара, т. е. все центры конденсации должны образовываться из самих пересыщенных паров. Образование тумана — дисперсной системы из капелек жидкости — вследствие объемной конденсации состоит из четырех стадий: пересыщение пара, образование зародышей, рост зародышей за счет конденсации пара, коагуляция капель. Переохлаждение пара, как указывалось выше, достигается при разгоне потока из-за вдува массы. При определенном пересыщении в паре возможна спонтанная конденсация с образованием жидкости в виде капелек. Из термодинамики известно, что давление пара, находящегося в равновесии с каплей жидкости, тем больше, чем меньше радиус каплр. Значение критического радиуса капли, находящегося в термодинамическом равновесии с окружающим паром, можно определить по следующей формуле [51]: Капли, размер которых меньше критического, исчезают вследствие испарения, а капли размером больше критического растут. В переохлажденном паре в результате флуктуаций постоянно происходит образование комплексов различных размеров из нескольких молекул и их испарение [52]. В соответствии с характером процесса их образования чем больше размер комплекса, тем меньше их количество. Некоторые комплексы достигают размеров больше критических и становятся ядрами новой фазы. С увеличением пересыщения радиус зародышей уменьшается, а скорость их образования растет. К настоящему времени различные авторы при различных предпосылках получили большое число формул для расчета скорости образования зародышей [54]. Детальное кинетическое обоснование процесса конденсации в достаточно общем виде проведено Я. И. Френкелем. Для скорости образования капель критического размера им получена следующая формула [55]: (2.84) где m — масса молекулы; k — постоянная Больцмана. Формулы для скорости образования, полученные другими авторами в несколько ином виде, дают идентичные результаты. Представленные выше модели для описания состояния пара в дальнейшем использованы для анализа влияния принимаемой модели на расчетные параметры тепловой трубы. Сразу же отметим, что расчетная мощность трубы практически не зависит от принимаемой модели для описания состояния пара. Учет рассматриваемых факторов при описании состояния пара оказывает влияние на изменение рассматриваемых параметров парового потока по длине и, в первую очередь, на распределение температуры при наличии значительных осевых градиентов температуры. Значительные изменения температуры пара по длине трубы имеют место при работе на звуковом пределе мощности и при весьма интенсивном теплоотводе, когда хотя бы на части зоны конденсации реализуется сверхзвуковой режим течения пара. Для дозвуковых режимов течения пара, которые наиболее характерны при работе тепловых труб, модель идеального газа дает достаточную для технических расчетов точность при определении изменения параметров парового потока по длине тепловой трубы. Ивановский М. Н., Сорокин В. П., Ягодкин И. В. Физические основы тепловых труб.—М.: Атомиздат, 1978