ТЕЧЕНИЕ ЖИДКОСТИ В КАПИЛЛЯРНЫХ СИСТЕМАХ
В качестве фитилей тепловых труб могут использоваться различные капиллярно-пористые материалы; металлический войлок, прессованное металлическое волокно, пористые структуры, состоящие из нескольких слоев сеток, спеченные пористые материалы и т. п.
Капиллярно-пористые материалы — это твердые тела, содержащие большое количество пустот, характерный размер которых весьма мал по сравнению с характерным размером тела. Пористые материалы по структуре разделяют на упорядоченные и неупорядоченные. Примером упорядоченной структуры может служить пористый материал, полученный при правильной укладке шаров одинакового размера. Неупорядоченную структуру представляют собой, например, пористые спеченные материалы, состоящие из компонентов различного размера. Чаще всего в пористых телах пустоты распределены беспорядочно. Структура таких тел может быть описана статистически. Однако течение жидкости в этих телах удобно анализировать с использованием макроскопических характеристик, которые зачастую определяются опытным путем [1].
Основными характеристиками капиллярно-пористых тел при применении их в тепловых трубах являются: объемная и поверхностная пористость, проницаемость, эффективный радиус пор структуры при создании капиллярного напора, насыщенность жидкостью.
Объемная пористость определяется как отношение объема пор УПОр к объему тела У0:
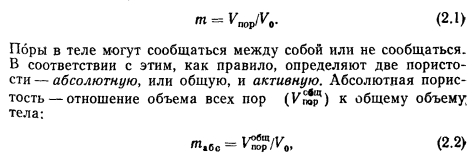
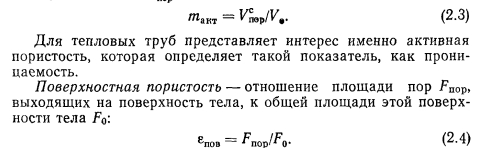
Удельная поверхность Fya пористого тела представляет собой площадь внутренних поверхностей пор, приходящихся на единицу поверхности объема тела. Она является параметром, определяющим проницаемость.
Проницаемость — свойство пористого материала, характеризующее его способность пропускать через себя жидкость под действием приложенного градиента давления. Проницаемость через измеряемые величины определяется по закону Дарси. Для пористого тела длиной / с площадью поперечного сечения F при протекании жидкости вдоль тела проницаемость можно определить по формуле

Часто пористые материалы обладают свойством анизотропности, т. е. проницаемость их в различных направлениях различна. Пример анизотропной капиллярной структуры — структура из сеток саржевого плетения: проницаемость для этой структуры различна вдоль и поперек основы сеток.
Предпринималось много попыток создать теорию, связывающую геометрическую структуру пористого материала с проницаемостью. В теории Козени [2] пористая среда представлена в виде связки капиллярных трубок равной длины. Исходя из решения классических гидродинамических уравнений для ламинарного установившегося течения, Козени показал, что проницаемость этой системы записывается в виде
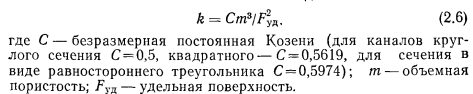
Для учета искривленности трубок тока в пористой среде иногда вводят понятие извилистости т. Извилистость определяется как отношение средней длины траектории жидкости в образце к длине образца. С учетом извилистости уравнение Козени может быть записано в виде

Трудности использования этою уравнения заключаются в том, что величины т и Куд взаимозависимы и определить их по отдельности весьма сложно. Значения безразмерной постоянной Козени С для различных образцов капиллярно-пористого тела с неупорядоченной структурой обычно определяются эмпирически и имеют значительный разброс.
Теория Козени широко используется при теоретических обобщениях, существует много ее модификаций. Следует отметить, что эта теория дает хорошие результаты лишь при малых значениях пористости, при большой пористости необходимо учитывать статистический характер распределения составляющих пористого материала.
Насыщенность жидкостью. Пустоты в пористом материале могут быть заполнены как жидким теплоносителем, так и его парами или газом. Насыщенность пористой среды Sc теплоносителем определяется как относительная часть объема пустот тела, занятая жидкостью, т. е.
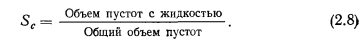
Рассматривая зависимость капиллярного давления от насыщенности среды жидкостью, отметим возможность существования гистерезиса — кривые капиллярного давления при впитывании жидкости и при осушении могут быть различны. Существование гистерезиса объясняется различными причинами. Контактные углы могут иметь различные значения в случае продвижения фронта жидкости в образец и при вытеснении жидкости из него. Это обстоятельство может быть связано с тем, что контактный угол изменяется со временем вследствие изменения свойств поверхности твердого тела под воздействием жидкости. Капиллярный гистерезис может быть обусловлен и самой геометрией пор. Так, гистерезис можно наблюдать в открытой капиллярной трубке с локальным сужением поперечного сечения. При медленном опускании такой трубки в смачивающую жидкость высота подъема жидкости сохраняется почти постоянной. При вынимании жидкость «задерживается» в месте сужения, а затем, когда капиллярные силы, возникшие за счет образования мениска в месте сужения оказываются недостаточными для уравновешивания гидростатического столба, Уровень жидкости скачком понижается.
Создание теории для описания течения в полностью насыщенной жидкостью капиллярной структуре, модификация уравнений в целях учета особенностей при неполном насыщении, описание гистерезиса — эти вопросы весьма актуальны для разработки капиллярных структур тепловых труб, для определения критических тепловых потоков, для исследования заполнения фитилей в гравитационном поле и невесомости. Их изучению посвящены, в частности, работы [3, 4], обзор некоторых результатов дан в [5], а в [1, 6—9] читатель найдет полезные сведения по рассматриваемому вопросу.
В капиллярно-пористых структурах тепловых труб, как правило, осуществляется ламинарное течение. Как уже указывалось, влиянием инерционных эффектов вследствие изменения массового потока жидкости по длине фитиля практически всегда можно пренебречь. При этих условиях применимо уравнение Дарси, которое в дифференциальном виде записывается как

Перепад давления в жидкости на длине трубы в фитиле определяется из уравнения (2.9) путем интегрирования при соответствующих граничных условиях. Для фитиля постоянного сечения F, полностью насыщенного жидкостью, имеем
В общем случае приходится искать перепад давления в жидкости на расстоянии от начала зоны испарения (точка 0) до мокрой точки. Когда массовый расход жидкости в фитиле изменяется линейно от нуля до максимальной величины, а мокрая точка находится в конце зоны конденсации, определяется как
Ивановский М. Н., Сорокин В. П., Ягодкин И. В. Физические основы тепловых труб.—М.: Атомиздат, 1978
