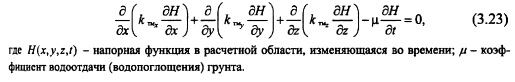ОСНОВЫ ТЕОРИИ ФИЛЬТРАЦИИ ВОДЫ
Водоподпорные сооружения (плотины, здания ГЭС, находящиеся в напор ном фронте, шлюзы, рыбоходы и т.д.) испытывают не только разницу давлении воды со стороны верхнего и нижнего бьефов (напор), но и давление воды, движущейся под действием этого напора по порам грунта основания и тела грунтовой плотины (п. 2.3). В этом случае различают две силы: взвешивания и фильтрационную, Движение воды в скальных основаниях имеет свои особенности,
В зависимости от состояния воды в порах грунта различают воду в виде:
а) водяного пара;б) гигроскопической воды, конденсирующейся на поверхности частиц;
в) пленочной;
г) свободной.
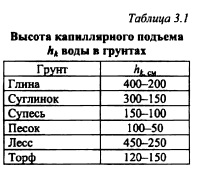
Максимальная гигроскопичность может быть: у песков до 1%, у пылеватых частиц до 7%, у глины до 17%. Пленочная вода образуется на поверхности частиц грунта под влиянием молекулярных сил. Она удерживается на поверхности частиц с силой, значительно превосходящей по интенсивности силу тяжести. Эту воду часто называют связной. Связная вода в грунте отличается по своим свойствам от обычной (меняются температура кипения и замерзания, вязкость, теплоемкость и т. д.). Ее можно отжать из грунта при давлении в несколько десятков и даже сотен МПа с одновременным подъемом температуры. Связная вода имеет пониженную растворяющую способность. Связная вода затрудняет фильтрацию, уменьшая сечение пор грунта. Влажность грунта, соответствующая максимальному содержанию пленочной (связной) воды, названа А.Ф. Лебедевым максимальной молекулярной влагоемко стью. В свободной воде выделяют гравитационную, передвигающуюся в порах грунта под влиянием силы тяжести (в ней действует только гидродинамическое давление), и капиллярную, на которую, кроме того, действуют капиллярные силы. Эта вода заполняет частично или целиком поры грунта и сверху ограничена вогнутым мениском (табл. 3.1) .
Гравитационную и капиллярную воду называют часто грунтовой водой.
Истинная структура грунта значительно сложнее, чем представленная схема. В ней имеются коллоидные вещества, откладывающиеся на поверхности минеральных частиц.
Эти коллоидные оболочки впитывают и химически соединяются с сорбируемыми водяными парами. Однако химическому взаимодействию имеется предел, после чего впитывание воды и разбухание коллоидных оболочек может происходить без химических реакций.
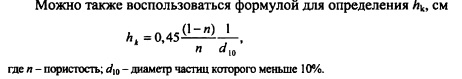
Таким образом, частицы влажного грунта имеют гигроскопическую оболочку. Затем с дальнейшим увлажнением они приобретают пленочную воду. В действительности частицы часто плотно сжаты между собой, что ограничивает развитие пленочного слоя. Слои вокруг частиц соединяются между собой, образуя в порах просветы, по которым может перемещаться вода. Но передвигаться может только гравитационная (грунтовая) вода. Движение грунтовой воды по суженным связной водой порам или трещинам в скальном грунте называется фильтрацией.
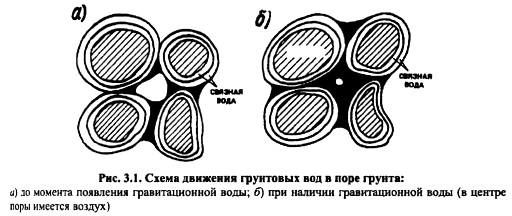
На рис. 3.1 дана схема движения грунтовых вод. На рис. а вода еще не стала гравитационной, и внутренняя область заполнена воздухом, а на рис. 3.1, б вода заполнила пространство между частицами, т. е. появилась гравитационная вода, но остался пузырек воздуха. Воздух фактически всегда присутствует в воде.
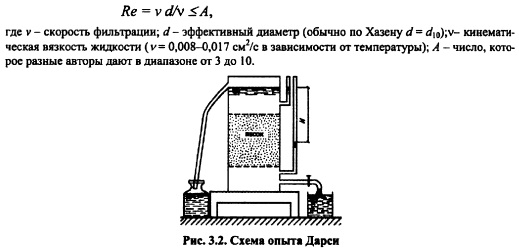
Экспериментальное исследование водопроницаемости грунтов. Начало развития теории фильтрации положил А. Дарси (1803-1858 гг.) своими экспериментами по фильтрации в образце песка, помещенном в цилиндр (рис. 3.2). Результаты своих экспериментов он изложил в книге, вышедшей в 1856 г. Он установил простейший закон движения воды в песке, который сформулировал следующим образом: «...Повидимому, для песка одного и того же качества можно допустить, что пропускаемый им расход пропорционален напору и обратно пропорционален толщине фильтрующего слоя». Если напор разделить на толщину фильтрующего слоя, то получим средний градиент напора и обычно закон Дарси формулируется так: «Скорость фильтрации пропорциональна градиенту»:

Многочисленные исследования фильтрации в мелких грунтах подтвердили выводы, сделанные А. Дарси. Коэффициент фильтрации имеет размерность скорости, т.е. он равен скорости фильтрации при градиенте, равном единице. Но линейный закон Дарси (3.1) имеет пределы применимости. Верхний предел применимости выражается числом Рейнольдса (Н.Н. Павловский, 1922 г.)
Существует и нижний предел применимости закона Дарси, когда сильно сказывается действие молекулярных сил.
Если число Рейнольдса оказалось больше 10, то используют более сложные физические уравнения, чем закон Дарси, например полином второй степени
Условие (3.3) удобно в применении с использованием ЭВМ.

Иногда считают, что в плотных глинах наблюдается так называемый начальный градиент напора, т. е. фильтрация начинается лишь при градиентах выше /о. В этом случае закон Дарси записывается в виде
Однако многие исследователи считают, что начальный градиент отсутствует, а имеет место нелинейный закон фильтрации (не выполняется нижний предел допустимости закона Дарси). Отметим, что отклонения от закона Дарси также возможны в области контактной фильтрации в трещиноватых породах основания и крупнообломочных грунтах, образующих взрывонабросные плотины.
Ориентировочно коэффициенты фильтрации некоторых грунтов даны в табл. 3.2.

Коэффициент фильтрации глинистых грунтов (глины, суглинки, супеси) может меняться во времени в результате изменения агрегатной структуры грунта и химической суффозии (см. п. 3.3).
В общем случае коэффициент фильтрации зависит от температуры вода, например, по Хазену, (0,7 + 0,03°), где Аю коэффициент фильтрации при 10° С.
Уравнения движения грунтовых вод. В каждой из пор грунта движущаяся вода имеет свой по значению и направлению вектор скорости. Меняются от поры к поре и ускорения. Это делает невозможным изучение скорости отдельных частиц воды для оценки общей картины движения воды в пористой среде. Удобнее рассматривать осредненные скорости в некотором объеме. Задача еще более упростится, если мы условно примем, что вода заполняет весь объем, включая объем, занятый минеральными частицами. В этом случае будем иметь сплошной поток, движущийся с фиктивными скоростями, так как действительные осредненные скорости будут больше за счет того, что действительный поток движется только по порам. Если выбрать в системе координат ось z, направленную вертикально вверх, то уравнения установившегося движения Эйлера [89] отдельных частиц жидкости в порах имеют вид:


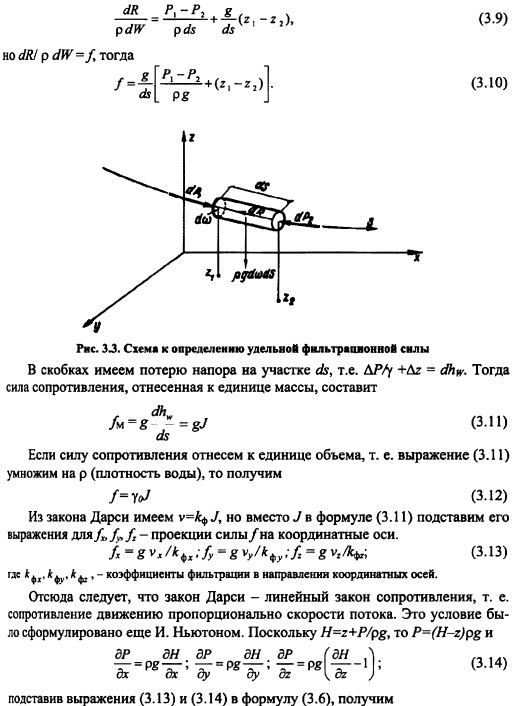

В скобках имеем потерю напора на участке ds, т.е. АР/у +Az = Тогда сила сопротивления, отнесенная к единице массы, составит
Если силу сопротивления отнесем к единице объема, т. е. выражение (3.11) умножим на р (плотность воды), то получим
Отсюда следует, что закон Дарси линейный закон сопротивления, т. е. сопротивление движению пропорционально скорости потока. Это условие было сформулировано еще И. Ньютоном. Поскольку H=z+P/pg, то P=(Hz)pg и
Уравнения (3.16) носят имя H.E. Жуковского. Практически Н.Е. Жуковский аналитически вывел уравнение Дарси.
Из курса гидравлики известно условие сплошности установившегося потока
Подставив выражение (3.16) в формулу (3.17), получим основное дифференциальное уравнение установившегося движения:
Для решения фильтрационных задач необходимо уравнение (3.18) дополнить граничными условиями.
В подавляющем большинстве фильтрационных задач уравнение (3.18) может быть упрощено. Если продифференцировав уравнение (3.18) и вынеся за скобки кф, получим
Если и все эти коэффициенты фильтрации по координатам постоянны, т.е. не зависят от координат, то говорят об области с анизотропными свойствами. В обоих случаях область однородная.
Если k=j(x, у, z), то область неоднородная. Чаще всего гидротехники имеют дело с неоднородными анизотропными областями фильтрации, но практически всегда можно свести задачу к кусочно однородной изотропной области или даже к однородной изотропной области. Рассмотрим анизотропную область на примере плоской задачи. В этом случае уравнение (3.18) примет вид:
Если ось х расположена в направлении максимального значения к$, то в направлении t надо область уменьшить раз и мы получим новую изотропную область. Решив задачу в координатах x и у перейдем в первоначальную систему координат х и у. растянув область в направлении х

При переходе из координат) к координатам нарушится одно из основных свойств гидродинамической сетки ее ортогональность, т.е. в анизотропной области жвипотенциали не ортогональны линиям тока.
На практике обычно решают задачи в плоской постановке, но имеется целый класс задач, когда надо решать пространственные задачи (например, фильтрация при строительстве гидротехнических сооружений, фильтрация под гидротехническими сооружениями при наличии в основании трещин).
Иногда требуется решать не только пространственные задачи, но и задачи с нелинейными законами фильтрации (например, при однородных по материалу плотинах, возводимых направленными взрывами).
Иногда требуется решать задачи неустановившейся фильтрации, что связано, к примеру, с колебанием уровня в водохранилище, с уплотнением водонасыщенных грунтов (см. гл. 12, §12.3) или при откачке или закачке жидкости в слои грунта.
В самом простом виде уравнение (3.18) в случае учета переменного напора приобретает вид: