СТАТИЧЕСКИЙ РАСЧЕТ АРОЧНЫХ ПЛОТИН
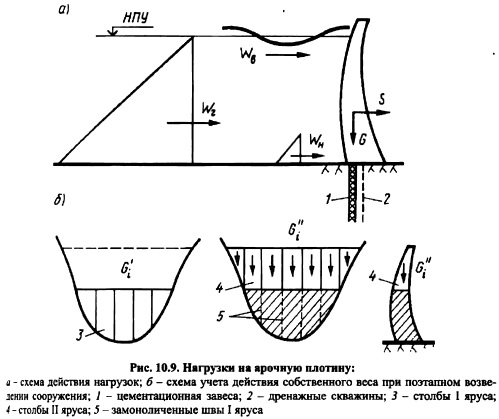
Силы, действующие на арочную плотину. Перечень сил и нагрузок, действующих на подпорные гидротехнические сооружения, приведен в гл. 2. Отметим некоторые особенности нагрузок, действующих на арочные плотины. В основное сочетание нагрузок для арочной плотины включают (рис. 10.9, а) гидростатическое и волновое давления воды собственный вес сооружения G, давление наносов и температурные воздействия.
Температурные воздействия существенно влияют на характер статической работы арочных плотин, которые являются статически неопределимыми системами. Усилия, возникающие в арочных плотинах от изменения температуры, могут быть соизмеримы с усилиями от гидростатической нагрузки, и явиться причиной нарушения монолитности сооружения. Подверженность арочных плотин температурным воздействиям заставляет применять специальные меры по борьбе с вредными их проявлениями.
Фильтрационное давление в основании плотины, обычно незначительное вследствие малой толщины плотины, а также сильно развитых цементационных завес и систем дренажа в основании сооружения, слабо влияет на характер статической работы арочных плотин. Следует, однако, учитывать значительную роль фильтрационных сил в расчете устойчивости береговых упоров арочных плотин.
Сейсмические (инерционные) силы входят в особое сочетание нагрузок. Наиболее опасное направление сейсмического воздействия в каждом конкретном случае требует своего определения. Для предварительного анализа можно пользоваться графиками рис. 17.14.
При статических расчетах нагрузка от собственного веса плотины должна приниматься с учетом схемы возведения сооружения (рис. 10.9, б). Арочные плотины возводят по ярусам в виде отдельных столбов, швы, между которыми по мере возведения сооружения после затухания температурноусадочных деформаций, замоноличивают.
Напряженное состояние арочных плотин возникает также вследствие деформации берегов и дна водохранилища под действием давления воды верхнего бьефа. Прогиб дна водохранилища и так называемый развал берегов ухудшают напряженное состояние арочной плотины, однако численная оценка указанного влияния затрудняется сложностью задачи, имеющей пространственный характер .
В задачу статического расчета входят расчет напряженного состояния арочной плотины и оценка устойчивости береговых склонов, воспринимающих нагрузки от сооружения.
Рис. 10.9. Нагрузки на арочную плотину: j схема действия нагрузок; б схема учета действия собственного веса при поэтапном возведении сооружения; 1 цементационная завеса; 2 дренажные скважины; 3 столбы 1 яруса; 4 столбы II яруса; 5 замоноличенные швы I яруса
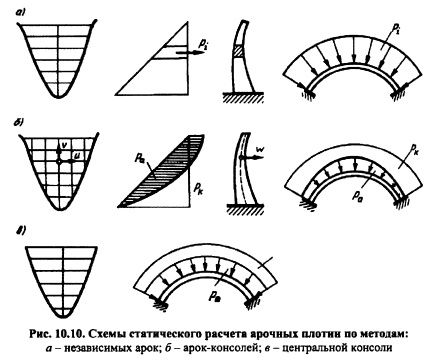
Методы статического расчета . Арочные плотины в статическом отношении представляют собой пространственную упругую оболочку с переменной кривизной и толщиной в вертикальном и иногда в горизонтальном направлениях, со сложными геометрическими и статическими граничными условиями. Точное определение напряженного состояния подобной конструкции встречает значительные математические трудности, что объясняет существование многих упрощенных методов статического расчета арочных плотин. Исходя из расчетных схем, в виде которых представляется арочная плотина, указанные методы могут быть объединены в следующие группы.
Метод, независимых арок. В данном методе расчетная схема арочной плотины представляется в виде отдельных независимо работающих горизонтальных арок, полностью воспринимающих действующую на плотину нагрузку (рис. 10.10, а). Наиболее приближенной формулой, применяемой для определения напряжений в отдельных арках, является так называемая котельная формула
Эта формула не учитывает условия заделки пят арок в берега, податливость основания и многие другие факторы, поэтому допускаемые напряжения в бетоне при расчете арочных плотин по котельной формуле ограничиваются низким пределом.
Метод независимых арок развивался в направлении уточнения расчета арки и учета условий ее опирания. Развитие метода расчета арки приведено в работах Н.Т. Мелещенко и A.JT. Можевитинова (расчет методом теории упругости); В.П. Скрыльникова и Р. Шамбо (учет сдвиговых деформаций); В.П. Скрыльникова, А.Стукки, А.А. Лосаберидзе (учет податливости основания у пят арки) и др.
Метод независимых арок применяется как приближенный для расчета сравнительно тонких арочных плотин в очень узких долинах, т. е. в случае, когда усилия в плотине передаются на берега в основном арочными элементами.
Метод, арокконсолей (комплексный метод). В этом методе (рис. 10.10, о) расчетная схема арочной плотины представляется в виде перекрестной системы из горизонтальных арочных и вертикальных консольных элементов, совместно воспринимающих действующую на плотину нагрузку.
В комплексном методе задача по существу сводится к разделению нагрузки на доли, воспринимаемые арочными элементами р° и консольными элементами р. Далее отдельно производят расчет арочных элементов на нагрузку р“ и консольных элементов на нагрузку р. Нагрузку разделяют из условия совместности (равенства) перемещений элементов в точках их пересечения.
В общем случае для каждой точки пересечения необходимо уравнивание перемещений и, V, w (тангенциальных, вертикальных и радиальных) и соответствующих углов поворота.
На практике в целях упрощения расчетов иногда ограничиваются уравниванием только одних радиальных прогибов и>, которые в наибольшей степени определяют характер разделения нагрузки. Кроме того, для предварительных расчетов уравнивание производят лишь по одной центральной консоли (метод арокиентральной консоли).
В методе характер распределения нагрузки, полученный из уравнивания прогибов ключевых точек арок и центральной консоли, распространяется на все остальные консоли. В этом случае нагрузка, действующая на арки, принимается постоянной по всей длине арки (рис. 10.10, в).
В методе арокконсолей (многих консолей) распределение нагрузки по длине арки устанавливается расчетом и в общем случае может быть неравномерным (рис. 10.10, б). В рамках комплексного метода применяют различные способы расчета перекрестных систем. Это привело к разработке ряда его вариантов: метод пробных нагрузок на основе ряда проб (последовательных приближений) задается распределение нагрузки между арочными и консольными элементами, обеспечивающее уравнивание перемещений в точках их пересечения; метод Риттера крыльникова распределение нагрузки отыскивается из решения системы алгебраических выражений, описывающих равенство прогибов в отдельных точках пересечения консоли и арок; метод Ганева используется идея замены перекрестной системы элементов расчетной схемой в виде одной системы элементов (консолей), лежащих на упругом основании, образованном второй системой элементов (арок).
Существует и ряд других способов расчета указанных систем, которые отображены в работах А. Розина и К. М. Хуберяна, А. М. Какушадзе и др. [7, 15]. На практике наибольшее признание из указанных методов получил метод пробных нагрузок, в котором более полно учитываются факторы, определяющие работу консольных и арочных элементов плотины. Метод этот чрезвычайно трудоемок, несмотря на наличие ряда таблиц, облегчающих расчет. Однако он дает положительные результаты, правильность которых подтверждена наблюдениями на построенных плотинах и опытами на моделях. С применением ЭВМ расчеты по данному методу значительно облегчаются.
Метод, теории оболочек, представляющий арочную плотину как сплошное упругое тело, характеризуется значительными математическими грудностями. Его развитием занимались Ф. Тельке, Е. Ломбарди, М. Герцог, Х.Ганев, И. Гудушаури и др. В настоящее время в связи с применением ЭВМ юявилась возможность практического использования данного метода для рас эета арочных плотин. В этом случае решение задачи осуществляется методом конечных разностей [55] или методом конечных элементов [57].
В послевоенные (шестидесятые) годы большое развитие получили исследования напряженного состояния арочных плотин на моделях, изготовляемых из упругих материалов (оргстекло, эпоксидные смолы) и материалов, подобных бетону (гипс, пемзобетон, керамзитобетон и др.). Экспериментальные исследования позволяют не только изучать напряженное состояние арочных плотин с учетом нелинейного характера поведения бетона под нагрузкой и реального строения скального основания, но и определять запасы прочности и схемы возможного разрушения сооружения при увеличении на модели действующих нагрузок. Экспериментальные исследования позволяют апробировать конструкцию плотины, запроектированную на основе аналитических расчетов (подробнее см. гл. 32).
В настоящее время приближенные методы расчета (метод арок центральной консоли и др.) применяются лишь на предварительной стадии проектирования. На завершающей стадии проектирования расчет арочных плотин I и П классов высотой более 60 м рекомендуется выполнять в объемной постановке совместно с основанием с применением метода конечных элементов, а также на основе экспериментальных модельных исследований.
Учет податливости основания в расчетах арочных плотин. При расчетах арочных плотин или отдельных ее элементов (арок и консолей) в зависимости от конструкции плотин и жесткости (податливости) основания задаются различные граничные условия по контуру сопряжения сооружения с основанием.
В случае заделки арочной плотины в берега наиболее просто решается задача расчета при задании жесткого защемления по контуру опирания сооружения, перемещения арочной плотины по контуру ее опирания. Простая схема расчета сооружения в этом случае объясняет распространенность данных граничных условий.
Вместе с тем многочисленные исследования (теоретические и экспериментальные) указывают на существенное влияние податливости основания на напряженное состояние сооружения. В арочных плотинах увеличение податливости основания, вызывающее увеличение перемещений плотины, обычно благоприятно сказывается на их напряженном состоянии, приводя к снижению максимальных сжимающих напряжений, которые возникают в пяте арки.
Наиболее распространенным методом учета податливости основания является способ, предложенный Ф. Фогтом. По этому способу перемещение в сечениях контакта плотины с основанием определяется как среднее перемещение некоторой площадки упругого полупространства, загруженной силами, передаваемыми плотиной на основание в указанном сечении контакта.
Решение указанной задачи представляется через так называемые коэффициенты Фогта к1 к2 к3 и к5 (рис. 10.11). Параметры определяются по следующим зависимостям:

Коэффициенты Фогта определяют в зависимости от отношения размеров контактной площадки Ыа и коэффициента Пуассона Цо скалы основания (см. с. 229, рис. 10.4 работы [Б4]); приближенные значения этих величин вычисляют по выражениям:

Отношение размеров контактной площадки Ыа принимают одинаковым для всех сечений опорной поверхности плотины с основанием и определяют по развертке контактной поверхности плотны на плоскость и замены ее на эквивалентный по площади прямоугольник (см. с. 226, рис. 10.2 работы [15]).
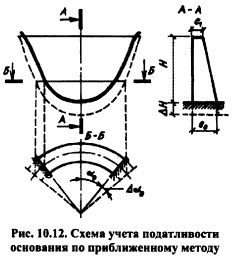
В некоторых схемах расчета арочных плотин используется более приближенный метод учета податливости основания по способу Фогта-Тельке. По приближенному методу производится фиктивное заглубление контура плотины в основание и ее жесткое защемление по фиктивному контуру (рис. 10.12). Размер указанного заглубления АН выбирают исходя из условия равенства перемещений плотины для фиктивно удлиненной жестко защемленной плотины и реального основания по действительному опорному сечению сооружения. Значение фиктивного заглубления для Еп/Ео=\ принимается равным (0,45+0,5) е0.
Расчет устойчивости береговых примыканий арочных плотин. Для надежной работы арочных плотин помимо обеспечения прочности ее конструкции должна быть обеспечена устойчивость ее береговых примыканий. Арочные плотины, опираясь на берега долины, передают на них значительные усилия. При недостаточно надежной врезке сооружения в берега под действием указанных усилий может произойти скол берегового скального массива или сдвиг его по ослабленным плоскостям в сторону нижнего бьефа.
Устойчивость береговых примыканий арочных плотин рассчитывается на основе рассмотрения предельного состояния выделенных из скального массива расчетных блоков [15,199].
При назначении формы и размеров расчетных блоков необходимо руководствоваться физически возможными положениями поверхностей сдвига, исходя из геологических, топографических и статических условий. При этом следует учитывать наличие геологических дефектов скального основания (крупных тектонических нарушений или трещин), очертание берегового массива (например, наличие резкого расширения ущелья в плане с низовой стороны плотины), значения и направления действующих усилий и т. д.
В проектной практике применяют метод расчета продольного сдвига береговых массивов по плоским поверхностям. В этом методе рассматривается сдвиг расчетного берегового блока (рис. 10.13), ограниченного двумя плоскостями сдвига и одной плоскостью отрыва по направлению линии пересечения плоскостей сдвига (линии сдвига). При расчете учитывают следующие нагрузки, действующие на опорный блок (см. рис. 10.13): Хл, Ка, 2, силы, передаваемые от арочной плотины при основном сочетании нагрузок; G собственный вес расчетного упорного блока; U\ U2, U2 силы давления фильтрационного потока на граничные плоскости. Кроме того, в составе нагрузок учитывают также сейсмические силы, как передаваемые от сооружения, так и непосредственно воздействующие на выделенный упорный блок.
При расчете все действующие силы приводятся к главному вектору R, который раскладывается на нормальные силы N1 и N2 (по нормалям к плоскостям сдвига) и сдвигающую силу Т (по направлению линии сдвига).

Коэффициент запаса устойчивости против сдвига (вдоль линии сдвига) определяется по формуле
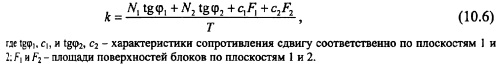
Коэффициент запаса устойчивости берегового упора массива, учитывая приближенность расчета, в зависимости от класса сооружения, рекомендуется назначать в следующих пределах [15, 199]: для основных сочетаний нагрузок 1,6+2,0, для особых сочетаний 1,25ч1,5.
Недостатком существующих методов расчета устойчивости береговых примыканий арочных плотин является то, что они рассматривают устойчивость берегового упора отдельно от арочной плотины, которая заменяется в этом случае нагрузками, передаваемыми от плотины в эксплуатационный период. В этом случае не учитывается сопротивление арочной плотины при возможном перемещении расчетного блока в предельном состоянии и изменение самих нагрузок, передаваемых от плотины при указанных перемещениях.
Более перспективным в оценке прочности береговых примыканий является направление, основанное на анализе напряженного состояния единого комплекса «арочная плотина основание». Указанное направление в настоящее время получает развитие в связи с возможностью решения сложных пространственных задач по определению напряженного состояния методом конечных элементов с применением ЭВМ.
