РАСЧЕТ НАПРЯЖЕНИЙ В ГРАВИТАЦИОННЫХ ПЛОТИНАХ МЕТОДОМ ТЕОРИИ УПРУГОСТИ
Основные положения. При расчете гравитационных плотин рассматривают плоскую задачу теории упругости. Данная задача в том случае, когда объемной силой является сила тяжести уб =ps g описывается следующими уравнениями [201]:
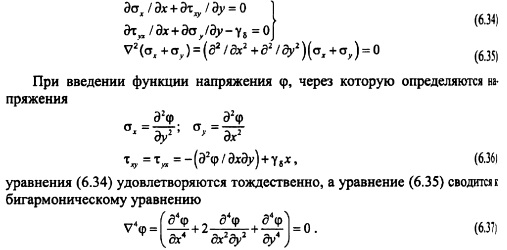
Таким образом, решение плоской задачи теории упругости в данной постановке заключается в нахождении функции напряжений ср, удовлетворяющей бигармоническому уравнению (6.37) и заданным уравнениям на контуре тела

В ряде случаев решение задач удобно выполнять в полярных координатах; соответствующие выражения, аналогичные приведенным выше, изложены в курсах теории упругости.
Расчет напряжений в плотине от гидростатического давления и собственного веса
Плотина представляется в виде бесконечного клина, загруженного собственным весом и гидростатическим давлением, при уровне воды на отметке вершины клина (рис. 6.8).
Для данного случая загружения функция напряжения принимается в виде:
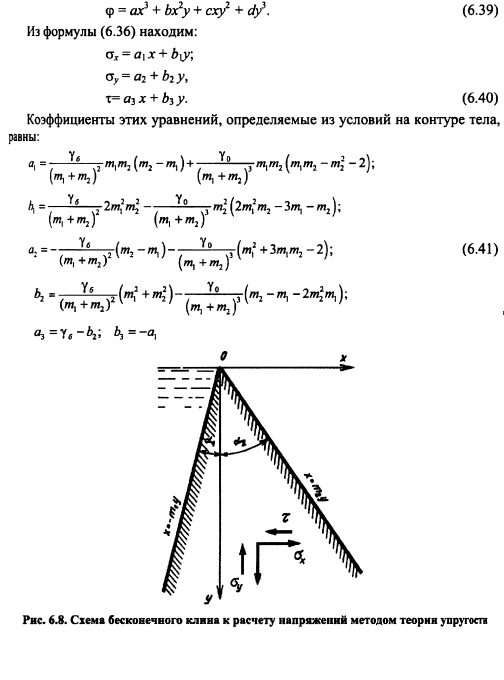
Коэффициенты этих уравнений, определяемые из условий на контуре тела, равны:
Если плотина не нагружена водой (строительный случай или опорожненное водохранилище), напряжения определяют по тем же уравнениям, но в ни надо подставит уо = 0, вследствие чего вторые члены выражений (6.41) отпадут.
По полученным значениям напряжений аоитв заданных точках внутри профиля плотины главные напряжения определяют по формулам (6.30) и (6.31), а направление их действия по формулам (6.32) или (6.33).
Изостату любого напряжения ст, оу и т строят по уравнениям напряжений (6.40) и (6.41). Для этого следует задать постоянное значение напряжения, например cr=const, и по уравнению для различных значений координаты х или у находить соответствующую другую координату той же точки.
Для упрощения построения кривых можно пользоваться следующим приемом. Из вершины треугольного профиля плотины проводят ряд лучей, считал за нулевой луч ось оу (рис. 6.9) и нумеруя их по порядку со знаком «+» направо от этой оси и со знаком «» налево.
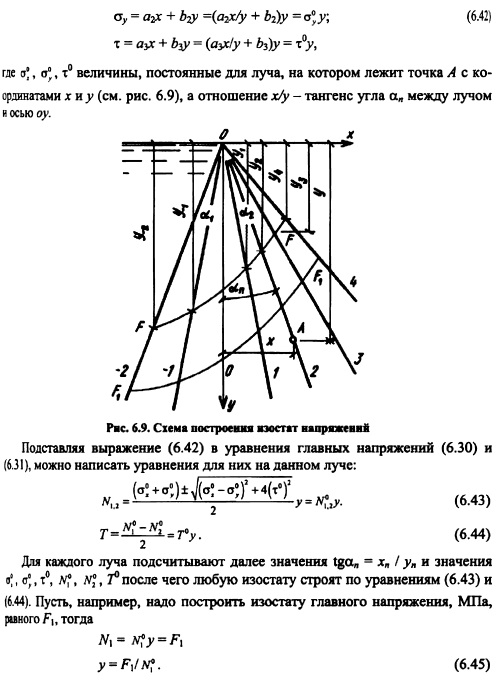
Подставляя в уравнение (6.45) значения для каждого луча, получают координату соответствующей точки заданной изостаты; соединяя эти точки от луча к лучу, строят кривую изостаты главного нормального напряжения (см. рис. 6.9). Давая другое значение N\, например F2, строят аналогичным путем кривую N= Fj Обычно изостаты напряжений строят для значений напряжений 0,5; 1,0; 1,5 МПа (5; 10; 15 кгс/см2) и т. д.
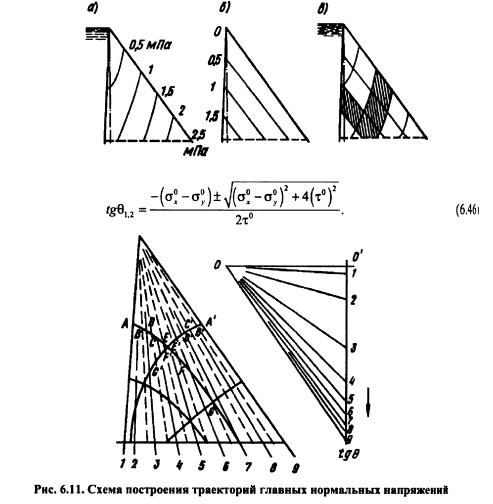
На рис. 6.10 приведены изостаты главных нормальных напряжений в плотине при наполненном (рис. 6.10, а) и опорожненном (рис. 6.10, б) водохранилище. Если совместить кривые первого и второго случаев на одном чертеже (рис. 6.10, в), то легко можно выделить зоны плотины, которые могут иметь напряжения в заданных пределах. Например, на рис. 6.10, в заштрихована зона с главными сжимающими напряжениями в пределах 1,5 МПа.
Кривыми изостат главных нормальных напряжений можно пользоваться для назначения в разных зонах плотины бетона соответствующей прочности.
Траектории напряжений. Положение площадок действия или направлений главных нормальных напряжений определяется углом наклона 0 этих площадок к оси Ох согласно уравнению (6.32). При этом значения tg0 вычисляют аналогично тому, как это делается для изостат главных напряжений, а именно: в выражение (6.32) подставляют значения стх, ау и т из уравнений (6.42). В результате получают формулу
Значение tg6 вычисляют по этой формуле для каждого луча, принимая знак перед корнем «+» для первого главного напряжения и «» для второго. Направления площадок напряжения графически наносят у соответствующих лучей. Практически для этого строят вспомогательный график (рис. 6.11), на котором откладывают направления векторов напряжений +01, +02, +03 по соответствующим значениям tgO (на рис. 6.11 для наполненного водохранилища), определяемым отношением и т. д. Затем, начиная от какойлибо грани профиля плотины, проводят линии на профиле, например ABCDEFG для напряжения N\ и A\B\C\D\E\F\G\ для напряжения N2, параллельные векторам и пересекающие соответствующий луч; длина этих лучей ограничивается биссектрисами углов, составляемых данным и соседними лучами (см. рис. 6.11). Таким путем может быть построен целый ряд траекторий в разных местах профиля плотины. Траектории главных нормальных напряжений N\ и N2 взаимно ортогональны, что следует из свойств этих напряжений.
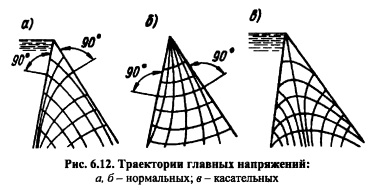
На рис. 6.12 показаны сетки траекторий наибольших и наименьших главных напряжений для случаев наполненного (рис. 6.12, а) и опорожненного (рис. 6.12,6) водохранилища и траектории главных касательных напряжений (6.12, в), при наполненном водохранилище. Траектории главных касательных напряжений направлены под углом 45° к траекториям главных нормальных напряжений.
Траектории главных касательных напряжений до известной степени характеризуют линии возможных разрушений бетонной кладки. Учитывая, что временные строительные швы бетонирования являются ослабленным местом кладки, стремятся чтобы их расположение не совпадало с траекториями главных касательных напряжений. В этом отношении швы при столбчатой разрезке плотины (см. рис. 8.11) близки к траекториям скалывания, что нежелательно; для восприятия скалывающих напряжений устраивают усиленное штрабление шва (см. рис. 8.12).
Расчет напряжений в плотине треугольного профиля от равномерно распределенной нагрузки на грани. В некоторых случаях грань плотины может быть нагружена равномерно распределенной нагрузкой, направленной под некоторым углом к грани (рис. 6.13). Такая задача была решена М. Леви, при этом выражения напряжений получены им отдельно для нормальной р и касательной рг к грани составляющих нагрузки р.
Напряжения определяются для отдельных лучей, проведенных из вершины профиля плотины под углом а к оси координат Оу. Характерно, что эти напр жения зависят только от угла и геометрических параметров профиля (см. рис 6.13): си, схг, tgai, mi = tgci2, т. е. постоянны по всему лучу.
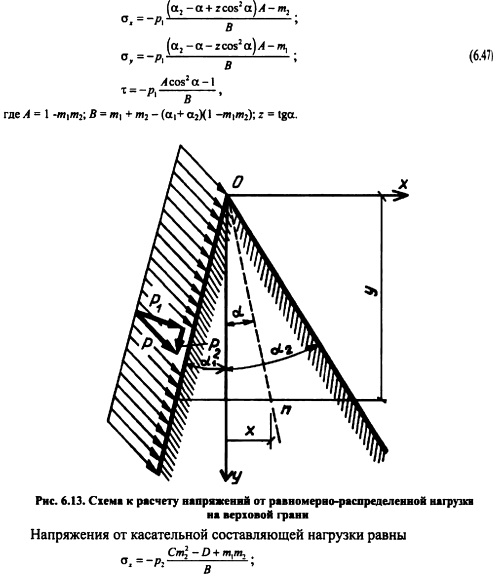
Напряжения от нормальной составляющей нагрузкив точке равны :
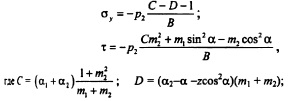
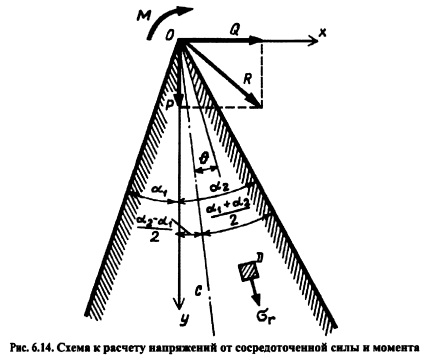
Расчет напряжения в той же плотине от действия сосредоточенной силы, приложенной в вершине профиля. Эта задача была решена Дж. Мичел лом в полярных координатах с началом их О в вершине треугольного профиля (рис. 6.14). Ось полярных координат ОС проходит по биссектрисе угла углы лучей 0 отсчитываются от этой оси. К оси прямоугольных координат Оу ось ОС наклонена под углом.
Напряжения от силы R, приложенной к вершине профиля О, на элементарной площадке в точке Д на луче OD обозначим стг в радиальном направлении тангенциальном.
На практике приходится определять напряжения отдельно от вертикальной Ри горизонтальной Q составляющих силы R (см. рис. 6.14).
Напряжения, вызванные силой Р, равны:

В выражениях (6.49) и (6.50) величина z=tga=xly, где а угол, составленный лучом OD с осью у прямоугольных координат, ахи у координаты рассматриваемой точки D, для которой определяются напряжения ar. По напряжению аг определяются напряжения в точке D в системе прямоугольных координат
Расчет напряжений в той же плотине от действия момента, приложен ного в вершине профиля. При обозначениях на рис. 6.14 (положительный момент по часовой стрелке) напряжения выражаются формулами
Расчет напряжений в плотине трапецеидального профиля. Реальные профили гравитационных плотин отличаются от треугольника, и в частности, для водосливных плотин приближаются к трапецеидальному (см. рис. 6.5). Метод решения задачи о напряженном состоянии трапецеидального профиля (в условиях плоской задачи), предложенный акад. Б.Г. Галеркиным, заключается в приведении этого профиля к треугольному и загружению его силами так. чтобы были удовлетворены заданные граничные условия трапецеидального профиля.
На границе АВ и ВС трапецеидального профиля (рис. 6.15, а) нагрузка отсутствует, а на напорной грани AD приложена гидростатическая нагрузка, которая может быть представлена в виде равномерно распределенной р0 и распределенной по закону треугольникар = у0(у И).
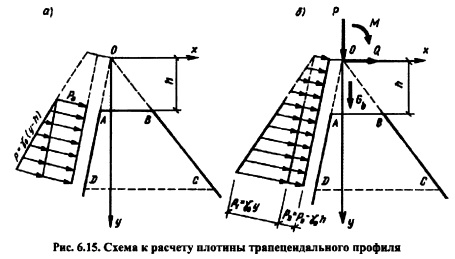
Напряжения в трапецеидальном профиле ст(стх, ау и т) будут определяться путем суммирования напряжений для треугольного профиля плотины от отдельных нагрузок
В данном методе для удовлетворения условий на контуре АВ принят принцип смягчения граничных условий (равенство нулю действующих усилий), что приводит к некоторым погрешностям лишь вблизи гребня плотины АВ, где напряжения вообще невелики; для всего остального профиля, согласно принципу СенВенана, решение будет достаточно точным.

Другие случаи загружения плотины. Используя прием Б.Г. Галеркина, можно рассчитать напряжения в плотине треугольного профиля от действия некоторых других нагрузок. Так, расчет напряжений в плотине при пониженной отметке верхнего бьефа, не совпадающей с отметкой вершины треугольного профиля (рис. 6.16 можно выполнить на основе суммирования напряжений от нагрузок, показанных на рис. 6.16,6

Подобным образом приближенно можно оценить влияние других нагрузок на напряженное состояние плотины.
