ПРЕДИСЛОВИЕ
Логическим развитием методов расчета конструкций и сооружений от детерминистических (по допускаемым нагрузкам и коэффициентам запаса) к по лувероятностному методу предельных состояний является переход к вероятностному методу расчета, учитывающего случайный характер нагрузок и воздействий, свойств строительных материалов и условий их эксплуатации. Вероятностный метод расчета развивается в рамках теории надежности инженерных конструкций и базируется на методах математической статистики и теории вероятности [13,96,169,].
Обозначим N любую из нагрузок и воздействий на сооружение, a S сопротивляемость, т.е. ту характеристику конструкции или свойства строительного материала, которая обеспечивает восприятие нагрузки N [83]. Вероятностный расчет сооружения заключается в определении вероятности безотказной работы Р, т.е. вероятности того, что параметр сопротивляемости S всегда больше параметра нагрузки N, и сравнение ее с нормативным значением вероятности Р":
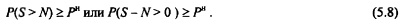
При выполнении условия (5.8) можно считать, что сооружение или конструкция отвечает требованиям надежности по рассматриваемому параметру.
В общем случае нагрузка и сопротивляемость являются независимыми случайными функциями времени, но в большинстве расчетов задачу удается упростить путем исключения из расчетов времени и представления S и N независимыми случайными величинами с определенными законами распределения.
Следует также отметить, что невыполнение неравенства в формуле (5.8) представляет собой отказ несоответствие нормативным требованиям, что в конкретных условиях влечет различные последствия: от просто невыполнения неравенства без внешних проявлений и нарушений работоспособности до разрушений в форме происшествия (с необходимостью небольшого ремонта) или аварии, катастрофы, бедствия в зависимости от последствий (5.9)
Вероятность безотказной работы Р и вероятность отказа V (риск) связаны очевидным соотношением
Например, водосливная плотина I класса но СНиП обеспечивает при ФПУ пропуск расхода обеспеченностью 0,01%, т.е. с вероятностью отказа (риском) F=0,0001, при этом вероятность безотказной работы Р=0,9999.
В большинстве случаев нагрузка и сопротивляемость определяются совокупностью большого числа воздействий и факторов, что позволяет принимать их распределения отвечающими нормальному закону (закону Гаусса) [56,77, 155];


Аналогично вычисляют среднюю арифметическую величину и дисперсию случайной нагрузки N, если она зависит от других случайных величин.
