Динамика развитая тепловых сетей в СЦТ
Практически при всех подходах к моделированию долговременного развития СЦТ наибольшие математические затруднения возникают при выборе оптимального распределения потоков теплоносителя в СЦТ. Основными трудностями при решении этой задачи являются: нелинейность физической связи между расходом теплоносителя и напором на границах участка теплопровода; существенное увеличение объема перерабатываемой информации по сравнению с оптимизацией структуры ИТ, так как совокупность ИТ в СЦТ и суммарная тепловая нагрузка СЦТ детализируются по районам теплопотребления; возможность изменения конфигурации ТС в процессе развития СЦТ за счет неравномерности роста тепловых нагрузок и мощности ИТ в тепловых районах.
Критерием оптимального распределения потоков теплоносителя в ТС служит минимум приведенных затрат по всей СЦТ в целом, который тесно связывает развитие ИТ в отдельных тепловых районах с изменением конфигурации и параметров ТС. С другой стороны, для выбора конфигурации ТС и диаметров ее отдельных участков неважно, какими ИТ создаются потоки теплоносителя; важны только объемы и темпмература транспортируемого теплоносителя, что позволяет, как отмечалось выше, декомпозировать общую задачу развития СЦТ на задачи развития ИТ в СЦТ и задачу развития ТС.
Основными целями моделирования долговременного развития ТС являются выбор последовательности конфигураций ТС по этапам планового периода развития СЦТ и количественная оценка сетевой составляющей приведенных затрат на развитие СЦТ, которая значительно сильнее зависит от изменения конфигурации сети, чем от изменения других ее параметров (пропускных способностей отдельных участков, определяемых соответствующим диаметром и напором; расположения, числа и параметров насосных станций и т.д.).
Как и при статическом подходе к моделированию СЦТ (см. гл. 4), возможны два метода выбора конфигурации ТС: традиционный, сводящийся к перебору и сравнению вариантов развития ТС, полностью намеченных проектировщиком, и оптимизационный, сводящий проблему выбора конфигурации к некоторой экстремальной задаче на схеме ТС. Математическая формулировка такой задачи определяется энергетической постановкой и учитывает необходимый уровень детализации модели, качество и полноту исходной информации, возможные математические трудности поиска решения (алгоритмическая сложность, высокая размерность и т.д.).
С энергетической точки зрения динамическая задача оптимизации конфигурации ТС формулируется следующим образом.
Заданы: число тепловых районов города и их размещение; тепловые нагрузки районов и необходимые выработки теплоты в начальный момент и по этапам (интервалам) планируемого периода развития СЦТ; число, типы и мощности действующих ИТ (для мелких котельных агрегирован- но по району) и их годовые выработки теплоты; типы, число и мощности блоков новых основных и пиковых ИТ и их возможные места расположения с учетом ограничений по условиям водоснабжения, экологии и тщ.; технико-экономические характеристики существующих ТС и возможные направления и условия прокладки вновь намечаемых участков ТС.
Требуется для каждого типа основного ИТ определить соответствующую последовательность конфигураций ТС по плановым интервалам, включающую: число, тепловые мощности и размещение основных и пиковых ИТ; направления и характеристики участков ТС от основного ИТ до тепловых районов.
Прежде чем переходить к математической формализации этой задачи, проанализируем специфику моделирования структуры СЦТ с учетом фактора динамики. Известно, что учет долговременной динамики ТС оказывает на экономический функционал такое же влияние, как и наличие существующей части сети [36], и приводит к существенной неаддитивности экономического функционала. Это может вызвать появление замкнутых циклов в оптимальных конфигурациях, невозможных при оптимизации СЦТ в статике. Здесь под аддитивностью экономического функционала понимают возможность представить его в виде суммы не зависящих друг от друга слагаемых, равных приведенным затратам на соответствующем интервале планирования. В динамике приведенные затраты на одном интервале времени зависят от совокупности всех предшествующих и последующих затрат, так как возможно изменение потокораспределения теплоносителя в процессе развития СЦТ. В вычислительном отношении неаддитивность целевого функционала является серьезным препятствием для применения методов динамического программирования.
Если учесть, что уже статические модели совместной оптимизации производительностей ИТ и конфигурации ТС относятся к классу многоэкстремальных задач нелинейного программирования (а при учете дискретности допустимых диаметров и других технических ограничений — к еще более сложному классу задач) высокой размерности [11], то становится очевидным, что в отсутствие быстрых алгоритмов динамического программирования формальное применение оптимизационного подхода к задаче динамики сети (т.е. основанное на нелинейных моделях ТС) сталкивается с непреодолимыми вычислительными трудностями.
В математическом отношении статические модели сводятся к минимизации вогнутой функции, определенной на выпуклом многогранном множестве допустимых потоков, удовлетворяющих материальным балансам сети. Точками минимума вогнутой функции являются некоторые граничные точки этого многогранника (его вершины). Так как линейные функции также достигают экстремума в вершинах многогранника допустимых потоков, появляется возможность использовать соответствующую линейную модель для поиска оптимального потокораспределения.
Применение линейных моделей для задач перспективного планирования распределения потоков в сетях с нелинейным законом течения (газопроводов) описано в работах [23, 64]. В них указывается, что для целей перспективного планирования вполне достаточно указать значение средних производительностей отдельных участков сети, а уточнение результатов этих расчетов с помощью более точных моделей необходимо лишь для контроля реализуемости таких планов. Ввиду возрастающей неопределенности условий функционирования системы при планировании на достаточно отдаленные сроки такое упрощение математического описания вполне естественно.
Нами аналогичный подход применен для решения динамической задачи применительно к ТС. При этом удобно воспользоваться понятием пропускной способности сети как общей характеристики ее производственной мощности, пренебрегая зависимостью ее от напора на границах отдельных участков. Тогда задачей перспективного проектирования развития ТС становится выбор потокораспределения и приращений пропускных способностей участков ТС.
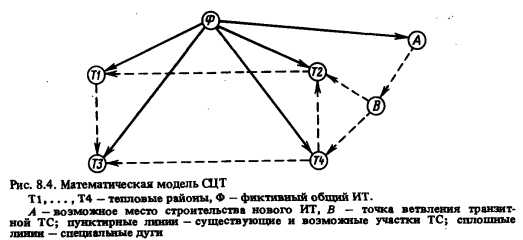
Как и в методе избыточной схемы (см. разд. 4.3), математической моделью СЦТ является ориентированный граф (схема теплоснабжения), содержащий вершины, соответствующие потребителям теплоты (тепловым районам), имеющимся к началу развития системы ИТ, возможным местам строительства новых ИТ и точкам ветвления трубопроводов (имеющихся и возможных), а также специальную, фиктивную вершину — общий ИТ (рис. 8.4). Эти вершины соединены совокупностью дуг (ребер) графа, состоящей из двух множеств (LI,L2): существующих и возможных участков ТС (с указанием соответствующих длин, условий прокладки, начальных пропускных способностей и т.д.) — L1 и специальных дуг —L2, соединяющих общий ИТ со всеми имеющимися ИТ и возможными ИТ в СЦТ. Каждая из дуг / этого графа характеризуется двумя числами в данный момент времени т: пропускной способностью (мощностью) дуги (ЩУ и потоком в ней (Й), который отождествляется с передаваемым (выработанным) количеством теплоты.
Требуется определить приросты пропускных способностей (AQ{) ПО интервалам прогнозного периода и потоки в участках сети, минимизирующие приведенные затраты на развитие и функционирование СЦТ. Математически эта задача может быть записана так: найти минимум

Математическая модель развития ТС (8.8)—(8.17) фактически позволяет оптимизировать (в рамках линейного приближения) схему теплоснабжения в целом. Учитывая, что линейная модель существенно упрощает реальные взаимосвязи элементов СЦТ, целесообразно использовать ее только для выбора оптимальной последовательности конфигураций ТС для соответствующего основного ИТ. Для этого из решения задачи (8.8) —(8.17) выбираются оптимальные значения переменных, определяющие потоки теплоносителя и последовательность конфигураций ТС. Далее согласно общей схеме решения задачи оптимизации СЦТ (см. гл. 4) решается задача оптимизации структуры ИТ в СЦТ при заданной конфигурации ТС. Если по совокупности общих оптимизируемых переменных моделей (8.1)-(8.7) и (8.8)-(8.17) полученные решения совпадают, т.е. совпадают мощность основного ИТ, момент его ввода, совокупная мощность пиковых ИТ и их выработка по интервалам планового периода, то получено оптимальное решение для данного типа основного ИТ. В противном случае корректируется исходная информация линейной модели по показателям ИТ и снова решается задача выбора конфигурации ТС. Детализация информации по ТС (число ниток трубопроводов, количество насосных и т.д.) для каждого интервала планирования проводится в рамках вариантного подхода (см. разд. 4.3).
В вычислительном отношении задача (8.8) — (8.17) достаточно проста и решается стандартными программами, входящими в математическое обеспечение ЕС ЭВМ, так как практически необходимая размерность задачи после декомпозиции по типам основного ИТ не превышает допустимых пределов при общей длительности периода развития СЦТ 15—20 лет и пятилетних плановых интервалах планирования.
Исследование систем теплоснабжения/Л.C. Попырин, К.С. Светлов, Г.М. Беляева и др. М.: Наука, 1989.
