Методика и алгоритм оптимизации
Задачи оптимизации внутренних параметров отдельных частей АСПТ (6.7) при фиксированных значениях параметров связи решаются независимо (см. разд. 6.1). В математическом отношении эти задачи относятся к классу задач нелинейного программирования. Процесс оптимизации ведется только по независимым переменным X, а соответствующие значения переменных Y определяются из решения системы балансовых уравнений. Без учета дискретного характера части независимых переменных и в предположении дифференцируемости функций цели 3 ( X) и учитываемых ограничений gt (X) каждый блок модели можно представить в стандартном виде задачи математического программирования:
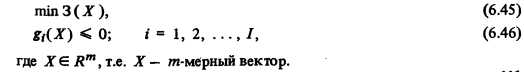
Если первоначально указанные блоки модели формируются в ином виде, например как задачи с двусторонними ограничениями, то путем формальных преобразований их сводят к стандартному виду.
Для поиска локального минимума в задачах нелинейного программирования имеется ряд методов, универсальных или учитывающих ту или иную математическую специфику входящих в описание задачи функций (выпуклость 3(ЛТ), вогнутость gf {X) и т.д.). Здесь использован метод, который можно отнести к классу алгоритмов проектирования градиента с восстановлением связей. Эти алгоритмы реализуют следующую схему вычислений.
1. В качестве начальной точки Х0 выбирается произвольная точка допустимой области, выделяемой в пространстве системой неравенств (6.45). Если начальная точка внутренняя, т.е. ни одно из неравенств не обращается в тождественный нуль, то делается шаг в направлении убывания функции 3(ЛТ).
2. На границе области допустимости среди направлений, гарантирующих убывание функции цели, определяется направление вдоль границы области и делается шаг определенной длины в этом направлении.
3. В случае выхода по направлению спуска из граничной точки за пределы допустимой области решается задача возврата на границу области допустимых решений.
Все алгоритмы данного класса по существу различаются лишь способами реализации шагов 2 и 3 описанной схемы вычислений. Спуск в направлении убывания функции цели (шаг 1) может быть реализован любым из градиентных методов. Общим свойством рассматриваемых градиентных методов при определении направления спуска в граничной точке Xк является проектирование градиента функции цели (точнее, обратного вектора — антиградиента) не на саму границу области допустимости, а на ее линейное приближение в этой точке. Это приближение получают линеаризацией тех ограничений в точке (их называют активными), которые выполняются как строгие равенства. Такой подход значительно упрощает реализацию второго шага схемы вычислений, заменяя поиск допустимого направления в линейной задаче более простой задачей поиска близкого к допустимому направления спуска.
Возврат в допустимую область также является важной вспомогательной задачей, так как поиск направления убывания целевой функции и возврат в допустимую область неоднократно повторяются в итерационном процессе поиска минимума и поэтому их алгоритмическая реализация должна быть достаточно простой. Ниже приводится математическое описание программной реализации этих вычислительных шагов.
Первая вспомогательная задача — поиск направления спуска. Для внутренних точек области допустимости применялась модификация градиентного метода, позволяющая не пересчитывать градиент на каждой итерации, если целевая функция убывает, а увеличивать вдвое шаг спуска, пока на некотором шаге значение функции не увеличится. Процедура спуска продолжается до выхода на границу области допустимости. На границе области допустимости возможны две ситуации: либо в некоторой точке существует касательная гиперплоскость к области допустимости, либо граничная точка является угловой. Если касательная гиперплоскость существует, линеаризация ограничений строится естественно. В угловых точках строится касательный конус К (рис. 6.5), образованный множеством векторов X, удовлетворяющих условию
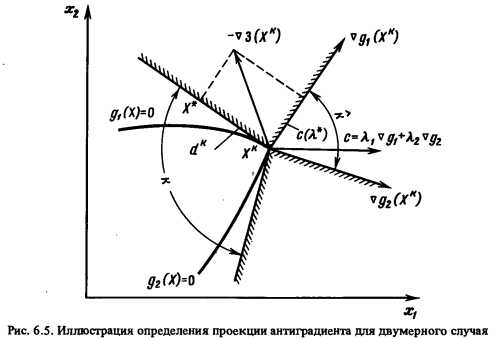

Если граничная угловая точка не является точкой минимума, то среди векторов касательного конуса найдется такое направление, вдоль которого целевая функция убывает. Можно показать [54—56] > что поиск наивыгоднейшего направления убывания целевой функции в окрестности точки Хк эквивалентен следующей задаче оптимизации:
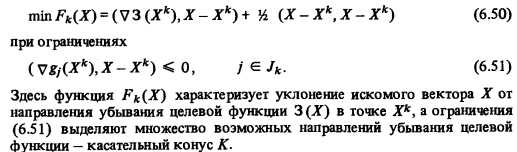
Здесь функция Fk(X) характеризует уклонение искомого вектора X от направления убывания целевой функции 3 (X) в точке Хк, а ограничения (6.51) выделяют множество возможных направлений убывания целевой функции — касательный конус К.
Задача (6.50), (6.51) является математической формализацией второго шага схемы вычислений поиска минимума в исходной задаче (6.45), (6.46). С целью уменьшения размерности в задаче квадратичного программирования (6.50), (6.51) (так как число активных ограничений меньше числа переменных X) и упрощения вида ограничений целесообразно перейти к эквивалентной двойственной задаче. Для этого строится функция Лагранжа!, (ЛГ, X):

Таким образом, задачу поиска направления уменьшения целевой функции удалось свести к задаче минимизации квадратичной формы с простыми ограничениями. Это позволяет при заданной точности вычислений вести поиск минимума одним из конечных методов, например методом сопряженных градиентов, который и был реализован в программе.
Вторая вспомогательная задача — возврат в допустимую область. Шаг по направлению, принадлежащему касательному конусу, может уменьшить значение целевой функции, но вывести из области допустимых решений. Известно [55], что, Выбрав длину шага достаточно малой, можно остаться на границе допустимой области. Для этого после каждого шага по проекции dk антиградиента — V 3 (Xfc) (6.55) вычисляются значения активных и неактивных ограничений. Если нарушаются неактивные ограничения, шаг уменьшается вдвое. Если нарушаются ограничения, которые на предыдущем шаге оставались активными, то осуществляется возврат на эти ограничения в точке X.
Исследование систем теплоснабжения/Л.C. Попырин, К.С. Светлов, Г.М. Беляева и др. М.: Наука, 1989.
