Оптимизация развитая систем теплоснабжения
Динамический характер задачи оптимизации развития СЦТ предопределяет необходимость получения решения, взаимоувязанного по всем интервалам рассматриваемого расчетного периода. Основной конечной целью решения оптимизационных динамических задач является нахождение наилучшей последовательности ввода в эксплуатацию и вывода из нее основных объектов рассматриваемой системы. Эта весьма сложная задача нелинейного программирования с дискретными переменными (см. гл. 8) еще больше усложняется при ее решении в условиях неполноты информации.
Большое значение для повышения достоверности исходной информации имеет использование принципа обоснования и принятия решений с минимально допустимой заблаговременностью. Этот принцип вытекает из свойства информации постепенно уточняться по мере приближения конкретного календарного срока, к которому она относится. Поэтому в случаях, когда имеется неопределенность выбора, окончательное решение следует принимать возможно позже, непосредственно перед началом его реализации. При этом будет использоваться каждый раз наиболее достоверная информация, имеющая минимально возможную неопределенность.
Практическое осуществление принципа минимальной заблаговременности требует соответствующей организации управления принятием решения. Так, при разработке и проектировании непрерывно развивающихся систем окончательное решение должно приниматься только по первоочередным объектам или для ближайшего интервала времени. По следующим объектам или интервалам времени окончательные решения следует принимать позднее, когда лучше прояснится реальная обстановка. При этом проектирование СЦТ будет представлять собой непрерывный процесс последовательного обоснования назревших первоочередных решений. Кроме того, целесообразно разбивать принятие решений на. этапы. Например, раздельно принимать решения о начале проектирования и о начале строительства объектов с параллельным проектированием нескольких конкурирующих объектов. При этом, с одной стороны, в процессе проектирования уточнятся технико-экономические показатели объектов, с другой стороны, за время, необходимое для проектирования, прояснятся внешние условия, что уменьшит неопределенность информации при принятии окончательного решения о строительстве объекта.
Осуществление непрерывного проектирования развивающихся систем требует четкого определения последовательности (очередности) принятия и взаимной увязки отдельных решений по развитию их объектов. Надлежащий учет неопределенности информации приводит к тому, что единая задача оптимизации развития СЦТ распадается на ряд задач (подзадач) обоснования отдельных решений, принимаемых в определенной последовательности и с соответствующей заблаговременностью. Каждая такая задача должна быть четко поставлена и увязана с другими задачами по времени (последовательности) решения и по составу обменной информации. В том числе должны быть уяснены связи рассматриваемой задачи с задачами развития систем более высокого иерархического уровня [9,27,91].
Как было отмечено в разд. 10.1, в настоящее время для решения динамических оптимизационных задач в условиях неполноты информации наиболее эффективен метод, базирующийся на использовании матрицы условия- решения. Общая последовательность этапов построения и анализа матрицы условия-решения для поиска оптимальных решений в динамических оптимизационных задачах та же, что и для статических задач, рассмотренных в разд. 10.2. Однако в реализации этих этапов имеются и существенные различия.
На первом этапе определяется состав неоднозначных исходных данных по СЦТ, которые создают неопределенность ситуации, и производится выбор ограниченного количества представительных сочетаний этих данных, те. формируется множество Мj. Общим критерием для отбора существенных показателей исходных данных, включаемых в множество Mj, служит тот факт, что при изменении значения показателя (в диапазоне его неопределенности) изменяется оптимальный вариант решения. Например, выбор того или иного объекта СЦТ в качестве первоочередного для строительства очень часто зависит от того, принимаются ли его экономические показатели (удельные капиталовложения или приведенные затраты) на верхней или на нижней границе диапазона возможных значений. Здесь же делаются экспертные оценки вероятностей принимаемых для расчета значений исходных данных и их сочетаний.
Второй этап включает выбор оптимальных решений для каждого из отобранных сочетаний исходных данных и анализ этих решений. Здесь очень важно четко определить смысл обосновываемого решения и состав характеризующих его параметров. Постановка оптимизационных динамических задач предполагает, что рассматривается длительный расчетный период, разбиваемый на несколько интервалов времени. В таких задачах, как правило, нужно различать первоочередные решения, для обоснования которых и ставится задача, и последующие решения, которые рассматриваются для определения последствий от первоочередных решений. Эти последующие решения могут быть различными для разных вариантов первоочередных решений и для разных условий развития систем. Параметры, характеризующие обосновываемые первоочередные решения, обозначим через Xi, а параметры, связанные с решениями на последующих интервалах времени, на которое разбит расчетный период.
Возможная схема принятия своевременных решений для развивающейся системы при разных условиях этого развития показана на рис. 10.2. Допустим, что календарю мы находимся в точке то, когда следует принять решения Хг и Хц о развитии системы. Интервал то — это интервал ближайших лет, для которого в силу ранее принятых решений (ЛГ0) и инерционности системы ее развитие в основном предопределено достаточно однозначно. Требуется принять решение о развитии системы на интервалах ту — Tj и тг — тз, когда эти решения уже могут активно воздействовать на ее развитие. Решения Xi, принимаемые для интервала ту — тг, являются первоочередными. Применительно к моменту времени т0 информация на интервале ту — т2 является существенно неопределенной; ее анализ позволил сформировать три представительных сочетания условий М и определить три возможных варианта развития системы по отрезкам

Аналогично изложенному в разд. 10.2 процесс поиска оптимального значения параметров Х зависит от состава неопределенной исходной информации, вошедшей в вектор Му. Здесь также можно выделить два характерных случая: а) в состав информации входят экономические показатели и показатели энергетической эффективности элементов СЦТ, изменение которых не отражается на соблюдении балансовых условий; б) неопределенными являются как экономические показатели, так и разного рода внешние технические факторы и расходные характеристики. Например, неопределенной является величина тепловой нагрузки СЦТ на конец интервала и тл. Ниже рассматривается более общий случай, когда при некоторых сочетаниях информации (из Mj ) для рассматриваемого варианта решения ХЦ не соблюдается часть технических ограничений или балансовых условий.
Каждому варианту условий Mj соответствует условно-оптимальное решение Хц по СЦТ, определяемое из задачи нелинейного дискретного программирования:

Метод решения задачи (10.14)—(10.16) изложен в гл. 8. Полученные условно-оптимальные решения заносятся в левый столбец матрицы условия- решения (табл. 10.3). Хотя непосредственный интерес представляют решения для первого интервала времени, т.е. Хц, для общности картины в матрицу внесены решения Хц, ..., XKi для всех интервалов рассматриваемого
периода. Минимальные значения приведенных затрат, соответствующие найденным условно-оптимальным решениям, располагаются по главной диагонали матрицы. Кроме условно-оптимальных решений, в матрицу могут быть включены для рассмотрения некоторые дополнительные ва- арианты решений, определяемые интуитивным путем разработчиком СЦТ.
Далее проводится анализ результатов с целью определения степени близости значений параметров Хц,..., Хц,..., Хц для рассмотренных условий My Mj. Сопоставление по приведенным затратам 3 дрсь неправомочно, так как найденные решения получены при различии «шит» условиях (например, разных годовых темпах роста нагрузки) и не могут йьт. приведены предварительно к тождественному энергетическому эффекту. Критерием близости полученных решений является степень последовательности вводов отдельных объектов СЦТ в эксплуатацию. При этом выделяются: а) основные существующие и новые объекты, вошедшие во все полученные решения для интервала Ту — т2 и с производительностью; б) то же, но с разной производительностью;

в) существующие и новью объекты, вошедшие только в часть решений;
г) новые объекты, не попавшие ни в одно решение.
Существующие и новые объекты, вошедшие (с равной или разной производительностью) во все решения, могут быть признаны абсолютно экономичными. Объекты, попавшие только в часть решений, являются сомнительными. По таким объектам необходим специальный анализ, уточняющий: а) исходную информацию, дополнительно конкретизирующую относительную экономичность спорных объектов; б) условия, позволяющие производить дополнительную независимую и более детальную оптимизацию таких объектов и др.
Иногда таким качественным анализом полученных результатов можно найти решения, которые позволяют считать данную оптимизационную задачу исчерпанной. Но в ряде случаев расхождение результатов расчетов оказывается столь существенным, что требует дополнительных расчетов. Точность этих расчетов можно существенно увеличить, если исключить из них объекты, вошедшие во все локально-оптимальные решения.
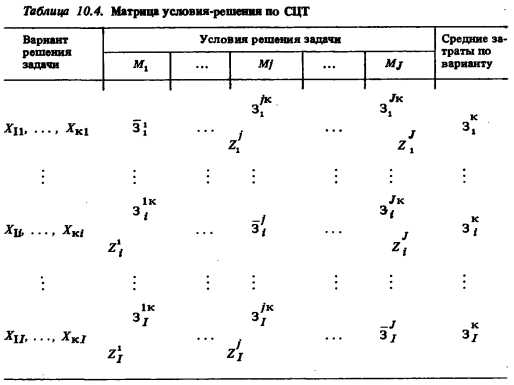
Дополнительные исследования зоны неопределенности решений включают заполнение матрицы условия-решения. Эта матрица дает возможность анализировать изменение денежных затрат при принятии данного решения, если условия развития СЦТ изменились в сравнении с теми, для которых принято данное решение. В заполненном виде матрица условия-решения приведена в табл. 10.4. Между табл. 10.3 и 10.4 может быть разница. При построении табл. 10.4 в отличие от табл. 103 предполагается существование реальной возможности перехода СЦТ от одного рассматриваемого условия к другому. В общем случае не для всех сочетаний решений Хц И условий Mj такое предположение справедливо.
Процесс заполнения матрицы условия-решения (табл. 10.4) не прост, так как необходимо не только оценить новое значение величины приведенных затрат для каждого элемента матрицы, но и обеспечить соблюдение всех ограничений и балансовых соотношений за счет выбор» в дополнение к основным решениям корректирующих мероприятий. Здесь под основными решениями — мерами по развитию СЦТ — понимаются те, которые заранее определены из нормальных оптимальных решений. Применительно к схеме принят? решений, приведенной на рис. 10.2, для момента времени т0 к основным решениям относятся решения Ху и Хц, принимаемые с достаточной заблаговременностью. Если задача оптимизации развития системы решается в момент времени т1г то основным является только решение Хц. Под корректирующими мероприятиями понимаются те, которые заранее не определялись; они должны осуществляться в связи с появлением новых, ранее неизвестных условий развития системы, требующих быстрой реакции, чтобы не нарушить нормального функционирования СЦТ. Естественно, что при прочих равных условиях корректирующие мероприятия относительно менее экономичны в сравнении с основными.
Рассмотрим процесс воздействия корректирующих мероприятий применительно к построениям рис. 10.2. Выше было определено, что применительно к моменту времени т0 наилучшим решением на втором и третьем интервалах является решение о развитии системы по отрезкам add2. Однако в течение интервала т0 — Ti выяснилось, что условия развития системы (например, рост ее нагрузки) изменяются; соответственно чтобы обеспечить бесперебойность теплоснабжения, необходимо провести некие мероприятия, например корректировку (в сторону ускорения) ввода мощности в пиковой котельной. В результате корректирующих воздействий к моменту наступления времени т2 СЦТ будет находиться в состоянии, характеризуемом не точкой d, а точкой d (приближенной к точке с, оптимальной для изменившихся условий развития).
Применительно к третьему интервалу разработчик, находящийся в интервале то — Tj, для исправления направления развития СЦТ может не только применять корректирующие мероприятия, но главным образом менять основные решения. В результате этих действий система по линии rfc выйдет к оптимальной точке с%. Однако на этом процесс оптимизации развития СЦТ не заканчивается. В самом деле, по истечении первого интервала времени, т.е, при функционировании СЦТ в интервале т2 — т2, произойдет дальнейшее уточнение исходной информации о развитии системы. Соответственно необходимо второй раз уточнить СЦТ на третьем интервале, но на этот раз в основном за счет корректируй} щих мероприятий.
Таким образом, процесс принятия решения о развитии СЦТ следует рассматривать как периодический процесс принятия основных решений (последовательно в точках т0, Ту, т2 и т.д.); между этими периодами часто требуется осуществлять корректирующие мероприятия, которые призваны реагировать на относительно частные изменения условий развития системы. Разумное сочетание корректирующих мероприятий применительно к ближайшему интервалу и возможностей пересмотра основных решений на последующих интервалах позволяет обеспечить достаточную гибкость развития СЦТ в условиях неопределенности информации.
Если конкретизировать указанные выводы применительно к практике разработки и проектирования СЦТ на 15-летний период, т.е. для трех последующих пятилеток, то получим следующее: развитие системы на первую пятилетку в силу ранее принятых решений и инерционности СЦТ считается в основном заданным однозначно и может лишь частично изменяться адаптивными корректирующими мероприятиями и путем корректирования затрат и сроков ввода переходящих объектов. Для второго пятилетия развитие СЦТ можно изменять, также преимущественно изменяя сроки и объемы ввода переходящих объектов корректирующими мероприятиями и лишь частично основными. Для третьего пятилетия можно принимать полноценные основные оптимизационные решения, естественно, в условиях частичной неопределенности. Как видно, учет фактора времени может существенно повлиять на процедуру и результаты заполнения матрицы условия-решения (см. табл. 10.4).
Наиболее часто причинами появления корректирующих мероприятий в СЦТ являются заранее неизвестные переходы к условиям с пониженными, одинаковыми или повышенными уровнями потребления тепловой энергии. В первом случае корректирующие мероприятия определяются наиболее просто — они сводятся в основном или к отказу от ввода соответствующего ИТ или участка тепловой сети, или к фиксации появления дополнительных резервов в системе. Изменение условий развития СЦТ при той же производимой тепловой энергии обычно требует перераспределения материальных и денежных средств внутри системы (например, на получение одного оборудования при отказе от другого). Наиболее сложно реагировать на изменения условий развития СЦТ, которые связаны с ранее неизвестным дополнительным ростом потребностей в тепловой энергии. В таких случаях источником корректирующих мероприятий могут быть только быстро реализуемые резервы производственных мощностей в пределах данной системы или дополнительный ввод даже менее экономичных ИТ.
Расчеты затрат по развитию СЦТ с учетом корректирующих мероприятий, вносимых в матрицу условия-решения (см. табл. 10.4), носят своеобразный оценочно-оптимизационный характер. Для рассматриваемого набора условий Му, ..., Mj все параметры (если нет нарушения ограничений) или их значительная часть (если имеет место нарушение ограничений при каких-то Mj) для каждого основного решения Хц, ..., Хку по СЦТ остаются неизменными. Элементы оптимизации встречаются лишь при выборе корректирующих мероприятий, характеризующихся вектором Z \ . Соответственно задачу оптимизации корректирующих мероприятий и вектора z[ можно записать следующим образом:
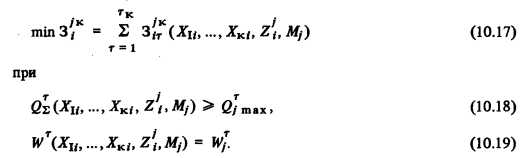
Данная задача аналогична ранее сформулированной задаче (10.14) — (10.16). Для несложных СЦТ совокупность корректирующих мероприятий, вектор Z и значения приведенных затрат могут быть определены на основе инженерной интуиции и простых расчетов. В более сложных случаях для решения задачи применим метод, изложенный в гл. 8.
Отметим одну принципиальную особенность матрицы условия-решения (табл. 10.4). В этой матрице к тождественности энергетического эффекта приведены лишь решения, записанные в столбцах матрицы (они получены для одинаковых условий развития СЦТ). Приведенные затраты, найденные при данном решении Xf = {.Хн, ..., XKi}, но при разных условиях Mj , т.е. по строкам матрицы, к такому тождеству энергетического эффекта не приведены. Таким образом, решение оптимизационных задач при неполной информации во многом изменяет подход к одному из основных требований оптимизационных детерминированных расчетов — предварительному приведению сравниваемых вариантов к тождественному энергетическому эффекту.
Для выбора по матрице условия-решения (см. табл. 10.4) лучшего решения по развитию СЦТ в настоящее время рекомендуется использовать критерий минимума средних затрат (по строкам матрицы). При этом решение по минимуму средних затрат совпадает с решением по минимуму среднего риска от незнания будущих условий развития системы. Минимум средних приведенных затрат находится по выражению (10.12) или (10.13) в зависимости от возможности количественной оценки вероятности появления условийMj .
Если величины средних затрат по некоторым строкам матрицы близки или даже совпадают, то решения, соответствующие этим строкам, следует рассматривать как равноэкономичные, практически неразличимые по приведенным затратам. Окончательный выбор решения из числа равноэкономичных должны делать специалисты по СЦТ с учетом преимуществ равноэкономичных вариантов по условиям гибкости, надежности, минимума затрат живого труда, экологических преимуществ и др.
Исследование систем теплоснабжения/Л.C. Попырин, К.С. Светлов, Г.М. Беляева и др. М.: Наука, 1989.
