Оптимизация источников теплоты

В результате решения задачи оптимизации ИТ и его оборудования определяется рациональная технологическая схема ИТ, оптимальные параметры и профиль оборудования, которые реализуются при сооружении ИТ. Возможности изменения, этих решений в случае существенного изменения условий функционирования ИТ очень ограничены или отсутствуют совсем. .В этом проявляется статический характер рассматриваемой задачи. Вместе с тем при поиске оптимальных решений по ИТ необходимо учитывать возможные изменения условий работы ИТ. Эти изменения за полный период эксплуатации ИТ, как правило, весьма значительны. Соответственно приходится решать статическую задачу в условиях динамики многих внутренних и внешних факторов.

Определение наилучших решений с учетом адаптации

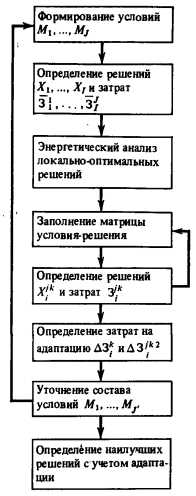
Оптимизационные расчеты ИТ при неоднозначной информации рекомендуется выполнять в три этапа: 1) выбор ограниченного, но представительного сочетания возможных условий создания и функционирования объекта; 2) выбор оптимальных решений для каждого из таких условий и их анализ; 3) обобщение полученных решений и формирование на этой основе зоны равноэкономичных решений по ИТ. Процедуры выполнения этих этапов существенно зависят от состава исходной информации, определяющей условия создания и функционирования ИТ и рассматриваемой как не полностью определенная. Здесь можно выделить два характерных случая: а) в состав учитываемой не полностью определенной информации входят экономические показатели (например, стоимость топлива, оборудования, материалов) , характеристики энергетической эффективности оборудования (например;

КПД котла) и другие показатели, изменение которых не отражается на работоспособности ИТ. Именно этот случай был рассмотрен в [91]; б) неопределенными являются не только экономические, но и внешние технические влияющие факторы (например, возможность перехода от сжигания малозольного к сжиганию многозольного топлива), изменение которых сказывается не только на экономичности, но и на работоспособности ИТ. Это более общий случай, применительно к нему также будет рассмотрена последовательность решения задачи (рис. 10.1).

Хотя отсев несущественной информации и снижает размерность задачи, часто она все же оказывается чрезмерно большой для практической реализации. Поэтому необходимо из данного множества возможных сочетаний исходной информации найти некоторое ограниченное, но достаточно представительное множество наиболее интересных для анализа условий создания и функционирования ИТ. В число таких сочетаний обычно вводят наряду с некоторыми средними (кажущимися наиболее вероятными) различные благоприятные и неблагоприятные сочетания, представляющиеся реально возможными. В процессе решения задачи набор принятых к рассмотрению условий будет уточнен (рис. 10.1).

Естественно, что каждому представительному варианту условий соответствует какое-то условно-оптимальное решение по ИТ. Это решение есть решение задачи оптимизации ИТ в детерминированной постановке:

Далее производится энергетический анализ полученных детерминированных условно-оптимальных решений с целью выяснения степени их совпадения. Поскольку конечной целью оптимизации ИТ является выбор оптимальной совокупности физических, расходных и конструктивно-компоновочных параметров, состава оборудования, а также вида технологической схемы объекта, то основной целью анализа полученных решений должно быть установление: а) степени совпадения результатов расчетов, т.е. выявление совокупности решений по составу оборудования, виду технологической схемы и величинам параметров, одинаковых или очень близких во всех вариантах исходных условий; все совпадающие решения могут считаться экономичными; б) необходимости более детальных оптимизационных расчетов (на основе дополнительно привлекаемой информации) для ряда элементов оборудования и значений параметров, а также для некоторых участков технологической схемы ИТ; в первую очередь уточнению подлежат решения, существенно различающиеся для рассматриваемых сочетаний исходных данных.

Анализ подобных условно-оптимальных решений может быть достаточен для решения задачи. Это имеет место, если оптимальные значения параметров и схемно-компоновочных характеристик ИТ оказываются близкими во всех рассмотренных вариантах условий. Если же окажется, что полученные решения существенно различаются по ряду важных компонентов, то необходимо продолжить процесс оптимизации, переходя к его третьему этапу.

Третий этап процесса оптимизации предусматривает проведение дополнительных расчетов с использованием матрицы условия-решения по ИТ (см. табл. 10.1). Речь идет о заполнении клеток матрицы, оставшихся свободными после определения и занесения в матрицу условно-оптимальных решений. Конкретно эта операция сводится к определению величины приведенных затрат 3{ на реализацию решения Xt при появлении сочетаний исходных данных, иных, чем то Mj, для которого решение Xt найдено как оптимальное. Для данного решения Xt значения 3 отличаются на величину ДЗ от 3 ; величину Д3 можно интерпретировать как затраты на приспособление (адаптацию) данного решения к соответствующим условиям.

Для случая, когда неопределенными являются только экономические факторы, заполнение матрицы условия-решения несложно; оно сводится к расчету (не оптимизации) ИТ и определению 3{ при тех или иных сочетаниях исходных данных. Различия производственной мощности объекта по столбцам матрицы, т.е. для каждого отдельного сочетания исходных данных Mj, имеющие место для разных вариантов решений, компенсируются с помощью замыкающих затрат на топливо, электрическую и тепловую энергию. При наличии соответствующей расчетной математической модели заполнение в этих задачах матрицы условия-решения не вызывает особых затруднений.

Процесс заполнения клеток матрицы условия-решения более сложен, если неопределенными являются не только экономические, но и внешние технические влияющие факторы. Дело в том, что в рассматриваемом случае нет гарантии работоспособности варианта решения задачи Xt, найденного для условий Mj, при всех остальных условиях. Иными словами, возможно нарушение ограничений по параметрам и технологическим характеристикам ИТ (10.2)—(10.5) при значениях Mi, . . . , Mj, отличных от М/, для которого решена задача (10.1)—(10.5) и найдено оптимальное значение Xt.

Необходимо проверить техническую работоспособность ИТ при всех вариантах значений параметров Xf применительно ко всем сочетаниям исходных данных Mj. Для тех вариантов локально-оптимальных решений Xj, которые при некоторых сочетаниях исходной информации Mj не удовлетворяют требованию работоспособности ИТ, необходима корректировка решений Xf.

Корректировка локально-оптимальных решений Х{ включает изменение физических и конструктивно-компоновочных параметров оборудования, вида технологической схемы и состава оборудования. За счет корректировки параметров Х{ достигается приспособление (адаптация) ИТ к новым условиям функционирования. Определение состава компонентов совокупности параметров Xt, подлежащих корректировке, — трудноформализуемая операция. Поэтому необходим инженерный анализ применительно к каждому из рассматриваемых сочетаний Mj и к каждому из локально-оптимальных решений Xt. Весьма часто в совокупность параметров Х{ приходится вводить новые параметры.

Реализация любого набора откорректированных параметров Х{к требует, как правило, дополнительных капитальных вложений или (и) приводит к увеличению текущих затрат по ИТ. Поэтому необходимо найти такой набор корректирующих параметров и такие их значения для каждого сочетания исходных данных М/, при которых приращение затрат по ИТ было бы минимальным. Для решения этой задачи используются обычные методы поиска наилучшего решения для однозначно заданной информации:

Статический характер задачи оптимизации ИТ в сочетании с большой длительностью периода эксплуатации ИТ обусловливает своеобразие процесса реализации откорректированных параметров XjK. Опыт эксплуатации ИТ разных типов показывает, что возможности функционирующего ИТ адаптироваться к непредусмотренным проектом условиям весьма ограниченны. Это естественно, так как в отличие от развивающихся систем энергетики более высокого иерархического уровня ИТ не развивается; все элементы и технологические связи в нем однозначно заданы при его создании. Адаптация к новым условиям функционирующего ИТ сопряжена с заменой действующего или установкой дополнительного оборудования, изменением технологической схемы. Затраты на такую адаптацию во многих случаях оказываются столь большими, что от нее отказываются. Ситуация осложняется также тем обстоятельством, что необходимость адаптации ИТ к новым условиям, как правило, выявляется через достаточно длительный период времени (10—15 лет) после начала эксплуатации объекта.

Положение коренным образом меняется, если уже на стадиях разработки и проектирования ИТ заложить в него способность адаптироваться к возможным условиям на протяжении всего периода функционирования. Такую способность обеспечивают найденные оптимальные решения XjK. Откорректированную совокупность параметров XjK делим на две группы параметров: XfKl и Хк2. Параметры первой группы Х{к1 определяют решения по ИТ, в том числе и по обеспечению его адаптивности, реализуемые на стадии создания ИТ. Параметры Х12 определяют решение по адаптации ИТ к возможным в будущем изменениям условий, которые реализуются по мере необходимости в процессе его функционирования.

При заполнении матрицы условия-решения (табл. 10.2) естественно должны быть учтены обе группы параметров: Х/к1 и Х2. При этом если параметры второй группы Хк2 индивидуальны для каждого элемента матрицы, то из параметров первой группы Хк1 должен быть сформирован единый обобщенный для каждой строки набор параметров X. Совокупность параметров X? определяет условно-оптимальное решение рассматриваемой задачи с учетом первого этапа адаптации.

Двухэтапный процесс адаптации более полно учитывает реальные условия создания и функционирования ИТ и позволяет:

выбрать на первом этапе решения с учетом того, что дальнейшие решения будут приниматься позднее на базе информации, полученной к тому времени;

уточнить за время перехода от первого этапа ко второму реальность наступления и характеристики отдельных рассматриваемых условий;

обеспечить рациональное сочетание двух принципов принятия решения: принципа принятия заблаговременного решения, позволяющего достигнуть результата с меньшими затратами, и принципа откладывания решения до получения более полной информации.

Разница затрат по ИТ, найденных с учетом и без учета необходимости корректировки параметров объекта, определяет затраты на адаптацию к соответствующим условиям с целью обеспечения работоспособности ИТ. Затраты на адаптацию могут быть представлены в двух видах:

затраты на адаптацию по элементам матрицы условия-решения ДЗfK, найденные как разница затрат по ИТ с учетом и без учета необходимости корректировки параметров ; эти затраты можно, в свою очередь, разделить на две части: Д3к 1 — затраты, производимые на этапе создания ИТ для обеспечения его адаптивности, и А3к2 — затраты, производимые в будущем для адаптации к изменившимся условиям;

затраты на адаптацию по строке матрицы условия-решения ДЗ, т.е. учитывающие необходимость однозначной реализации откорректированных параметров X на первом этапе адаптации, и по элементам матрицы Д3к2, т.е. учитывающие необходимость возможной реализации откорректированных параметров Xfx2 на втором этапе адаптации.

Изложенный подход к решению задачи оптимизации ИТ позволяет вернуться к этапу выбора состава рассматриваемых сочетаний исходной информации Mj и дать этому этапу экономическое обоснование. Как следует из приведенного, за возможность приспособления к новым условиям приходится платить уже на стадии создания ИТ независимо от того, наступят ли новые условия или нет, будут ли использованы заложенные в ИТ возможности к адаптации или нет. Очевидно, что в число рассматриваемых должны быть прежде всего включены те сочетания условий, вероятность наступления которых достаточно велика. Однако для всех сочетаний условий, т.е. как маловероятных, так и с большой вероятностью наступления, нужно сопоставить затраты на адаптацию ИТ А3(к к этим условиям и возможный ущерб Д3/у по ИТ или по соответствующей иерархически вышестоящей энергетической системе при отказе от адаптации ИТ к этим условиям. Величина ущерба А3{у должна оцениваться с учетом вероятности наступления соответствующих условий.

Целесообразность включения сочетания условий Mj для рассмотрения в матрицу условия-решения определяется соотношением

Сочетания условий Mj, не удовлетворяющие неравенству (10.11), должны быть исключены из рассмотрения (см. рис. 10.1). В их числе могут быть не только маловероятные сочетания условий. Если неравенству (10.11) не удовлетворяет сочетание условий М) с большой вероятностью их наступления, то это означает, что сделана не оправдавшая себя попытка найти единое решение, удовлетворяющее существенно различающимся условиям. При таком результате нужно рассмотреть целесообразность разработки двух различных по параметрам и характеристикам ИТ.

В результате заполнения матрицы условия-решения для второго случая получаем (см. табл. 10.2):

совокупность откорректированных оптимальных значений параметров ИТ Xf для каждой строки матрицы;

уточненную совокупность условий решения задачиМг,... ,Mf; совокупность оптимальных значений параметров ИТ Х[к2 для каждого элемента матрицы, определяющих направления адаптации объекта в период функционирования;

две пары составляющих затрат на адаптацию ДЗ/к1 и Д3/к2 или ДЗ иДЗк2.

Важно подчеркнуть, что благодаря корректировке параметров для каждого из вариантов решений обеспечена работоспособность при каждом сочетании рассматриваемых условий создания и функционирования ИТ. При этом матрица условия-решения приобретает определенное экономическое содержание, характеризуя по каждому оцениваемому варианту решения затраты как на его реализацию, так и на приспособление к рассматриваемым условиям.

Для сравнения и выбора решений с помощью матрицы условия-решения в литературе предлагаются разные критерии. Для рассматриваемого класса относительно частных и вместе с тем массовых задач в качестве основного рекомендуется критерий минимума средних затрат, обеспечивающий примерную взаимную компенсацию (в массе решаемых задач) реализации благоприятных и неблагоприятных условий. При этом решение по минимуму средних затрат совпадает с решением по минимуму риска от незнания будущих условий создания и функционирования ИТ. Значения средних затрат по вариантам решения (по строкам матрицы) приведены в крайнем правом столбце матрицы условия-решения (табл. 10.1 и 10.2).

Критерий минимума средних затрат может применяться в двух модификациях. Если появление рассматриваемых условий равновероятно, то применяется критерий минимума среднеарифметических затрат (по строке матрицы условия-решения)

При использовании данного подхода состав и содержание элементов левой части матрицы условия-решения остаются неизменными. Меняется только правая часть матрицы: вместо одного столбца средних затрат по варианту будет несколько столбцов (по числу принятых наборов значений. Каждый из них заполняется согласно выражению (10.13) и соответствует одному из принятых наборов значений.

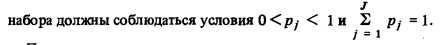
В результате дополнительного анализа зоны неопределенности оптимальных решений и выявления наилучших решений, отбираемых по критерию средних затрат, можно в частном случае найти единственное рекомендуемое решение либо в более общем случае значительно уменьшить размеры зоны. Входящие в оставшуюся зону неопределенности совокупности параметров следует рассматривать как имеющие равную экономичность, так как существующие формальные методы и приемы не позволяют осуществить их дальнейшую дифференциацию. Выбор окончательного решения из числа равноэкономичных требует привлечения дополнительных критериев оптимизации — технического совершенства решения, надежности работы, минимума затрат живого труда, социальных факторов и т.д.

Определенными возможностями дальнейшего сопоставления равноэкономичных вариантов обладает часто используемый прием [9, 20, 25], суть которого состоит в следующем. Пусть некое одно условие (или несколько условий) неопределенно настолько, что если оно примет значение Мх, то оптимально решение Хх с приведенными затратами 3 j; если же условие примет значение М2, то оптимально решение Х2 с затратами 32. Требуется определить предпочтительное решение (2fi или Х2) при равной вероятности появления условий Мх и М2. Решение задачи включает: а) определение дополнительных затрат ДЗл, которые необходимы в том случае, если принято решение Х% для условий Мх, а реально ИТ с параметрами Хх будет функционировать в условиях М2; б) рассматривается обратный случай — определяются дополнительные затраты Д32, которые необходимы, если принято решение Х2 применительно к условиям М2, а реальны будут условия Мх. Если величина Д32 > A3lt то целесообразно принять решение Хх, и, наоборот, при Д32 < ДЭц — решение Х2.

Анализ решения ряда задач оптимизации ИТ разных типов выявил закономерность: оптимальные решения, найденные в условиях неопределенности исходных данных применительно к неблагоприятному их сочетанию, обладают большей стабильностью и дают существенно меньший перерасход затрат при их реализации в условиях благоприятного сочетания исходных данных, чем решения найденные при благоприятных сочетаниях данных, но поставленные в условиях неблагоприятного сочетания исходных данных [20,25].

Исследование систем теплоснабжения/Л.C. Попырин, К.С. Светлов, Г.М. Беляева и др. М.: Наука, 1989.