ОПТИМИЗАЦИОННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И АЛГОРИТМ ОПТИМИЗАЦИИ

После выбора основных влияющих факторов и параметров необходимо построить оптимизационную модель СЦТ, учитывающую в качестве переменных лишь эти факторы и параметры. При этом второстепенным факторам и параметрам присваиваются фиксированные значения в допустимом диапазоне их изменения. В отличие от имитационной математической модели оптимизационная модель СЦТ должна учитывать зависимость критерия удельных приведенных затрат на тепловую энергию лишь от основных факторов и параметров, которые выявлены с помощью инженерного анализа и отсеивающих имитационных экспериментов на ЭВМ.

При построении оптимизационной математической модели многие авторы формально применяют аппарат регрессионного анализа, получая эту модель в виде полинома, как правило, не выше второго порядка [1, 64], а затем решают полученную задачу квадратичного программирования. Такой методический прием можно рассматривать в качестве одного из способов эквивалентирования математических моделей. Однако при этом коэффициенты уравнения регрессии не имеют четкого физического или экономического смысла, а полученная полиномиальная модель может оказаться многоэкстремальной, что во многом снижает целесообразность ее практического применения.

Поэтому представляется целесообразным построение оптимизационной математической модели СЦТ в аналитической форме с использованием зависимостей, имеющих определенный инженерно-экономический смысл. Для определения возможности корректного решения задачи оптимизации необходимо проверить полученную целевую функцию на одноэкстремальность, поскольку только в этом случае могут быть достаточно эффективны известные методы математического программирования.

Важным требованием является достижение максимально возможной простоты проведения комплексной оптимизации при сохранении основного содержательного смысла модели. Выполнение указанного требования достигается введением следующих предпосылок:

1. Оптимизационные модели разрабатываются отдельно Для водяных и паровых СЦТ.

2. Водяные СЦТ рассматриваются с двухтрубной закрытой и однотрубной открытой системами ГВС. Это стало возможным после получения результатов отсеивающих экспериментов и равноэкономичности СЦТ с двухтрубными закрытой и открытой системами ГВС, а также с зависимой и независимой схемами включения систем отопления. Однотрубная система изучается по схеме с двухтрубной тепловой сетью в пределах городской застройки. Регулирование отпуска теплоты осуществляется по графику с температурной надбавкой, что предполагает применение двухступенчатой последовательной схемы включения подогревателя ГВС для закрытой системы.

3. Для раздельной схемы энергоснабжения предполагается размещение районных водогрейных котельных на газомазутном топливе в пределах застройки (транзитные тепловые сети отсутствуют). В случае комбинированной схемы пиково-резервные водогрейные котельные размещаются на тех же площадках, причем тепловые сети от них остаются двухтрубными и для однотрубной системы.

4. При осуществлении комбинированной выработки электроэнергии на тепловом потреблении снижение потенциально возможной конденсационной мощности турбин вследствие недоиспользования перепада энтальпий между теплофикационными отборами и конденсатором практически не зависит от начальных параметров пара. При этом зависимость удельной недовыработки электроэнергии от температуры пара в отборе для различных давлений пара в конденсаторе с учетом ступенчатого подогрева сетевой воды близка к линейной [55]. Следовательно, изменения, вносимые отпуском теплоты из отборов турбин в баланс электрических мощностей энергосистемы, по сравнению с раздельной схемой энергоснабжения будут мало отличаться для различных типоразмеров турбин с различными начальными и одинаковыми конечными параметрами пара, установленных на электростанциях, работающих на различных видах топлива.

5. Выбор вида топлива, начальных и конечных параметров пара, единичных мощностей энергоагрегатов и электростанций в целом определяется главным образом тенденциями развития топливно-энергетического комплекса, его топливной и энергомашиностроительной базы. Поэтому предполагается, что имеется или строится крупная экономичная электростанция и рассматривается вопрос о целесообразности ее применения для целей теплофикации. При этом устраняется эффект разукрупнения единичных мощностей агрегатов ТЭЦ по сравнению с заменяемыми КЭС, что ставит комбинированную схему энергоснабжения в теоретически оптимальные условия в отсутствие экологических ограничений на размещение электростанции при дальнем теплоснабжении (в отличие от энергоисточников, размещаемых в непосредственной близости от города). Это дает возможность корректно упростить расчеты приведенных затрат, отнесенных на базовый источник теплоснабжения, путем определения их независимо от типа и состава основного оборудования электростанции, а также вида сжигаемого на ней топлива.

6. Незначительное влияние на экономичность СЦТ изменения в широких пределах единичной мощности тепловых пунктов позволяет не рассматривать их в оптимизационной модели СЦТ и определять капиталовложения во внутригородские водяные тепловые сети с помощью формул [421, которые аппроксимируют данные [56] для материальных характеристик водяных тепловых сетей в случае применения местных тепловых пунктов.

7. Капиталовложения в водяные тепловые сети определяются при оптимальных значениях диаметров транзитных трубопроводов и материальной характеристики внутригородских тепловых сетей с помощью известных формул [55, 42]. Таким образом, число непосредственно оптимизируемых параметров уменьшается на два, поскольку расчеты будут проводиться уже при оптимальных значениях удельного падения давления на трение как для транзитных, так и для внутригородских сетей.

8. Затраты на абонентские установки принимаются пропорциональными поверхности нагрева отопительных приборов [55].

9. Затраты на компенсирующую мощность в электроэнергетической системе, обусловленные отпуском теплоты из отборов турбин, оцениваются с помощью замыкающих затрат на электроэнергию.

10. Зависимость годового коэффициента теплофикации от часового представляется в виде аппроксимации обобщенных данных [2, 30, 54] полиномом второго порядка.

11. Тепловые потери в сетях и затраты на перекачку учитываются при определении диаметров трубопроводов и материальных характеристик.

12. Влияние ступенчатого подогрева сетевой воды на среднюю температуру пара в отборе учитывается по формуле, приведенной в работе [55].

13. В качестве основных факторов для оптимизационной модели СЦТ приняты: расчетные тепловые нагрузки в горячей воде QB и технологическом паре Qa, МВт; числа часов использования максимума тепловых нагрузок в горячей воде hB и технологическом паре hn, ч/год; длины транзитных водяных LB (приведенная) и паровых Ln (главная магистраль) тепловых сетей, м; средняя удельная теплоплотность застройки q, МВт/км2; замыкающие затраты на топливо для районных и пиково-резервных котельных , руб/т ; замыкающие затраты на компенсирующую электроэнергию Зэ0МП, руб./(МВт ч); коэффициент, характеризующий удельную стоимость тепловых сетей 6Т.С, руб./м2.

14. Основные параметры СЦТ, подлежащие комплексной оптимизации: коэффициенты теплофикации по нагрузкам в горячей воде ат и технологическом паре ап; отношение расчетных расходов сетевой воды в подающих линиях транзитных и внутригородских водяных тепловых сетей х = = G!p/Gp; расчетная температура сетевой воды в подающей линии внутригородских тепловых сетей тр, °С; рас. четная температура воды в обратной линии систем отопления Т20, °С (или перепад температур во внутригородской сети 6т, °С); расчетный перепад давлений в паровой сети Ара, МПа.

На основании анализа и обобщения данных различных авторов построена аппроксимирующая зависимость годового коэффициента теплофикации (атОД) от часового коэффициента (ат) и числа часов использования максимума тепловой нагрузки (гв):

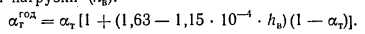
Замыкающие затраты на компенсирующую электроэнергию могут определяться тремя способами:

по замыкающим затратам компенсирующей электростанции в зависимости от числа часов использования ее мощности в энергосистеме /гкомп (для предпроектных расчетов можно принять /гкомп = К)\

по удельным издержкам производства (главным образом топливной составляющей) существующих электростанций, которые можно было бы вывести из эксплуатации при использовании рассматриваемой электростанции для производства только электроэнергии;

по разности замыкающих затрат на дополнительно вводимую базисную электростанцию и топливную составляющую вытесняемых ею существующих электростанций на органическом топливе по формуле (17).

Зависимость удельной недовыработки электроэнергии (э„) от расчетных температур сетевой воды в подающей tjp( °C) и обратной (tlp, °C) линиях транзитных тепловых сетей, а также давления пара в конденсаторе (7КОНд, МПа) п0 данным [55] для предпроектных расчетов аппроксимируется в следующем виде:

Составляющая удельных приведенных затрат на тепловую энергию, обусловленная недовыработкой электроэнергии за счет теплофикации, определяется по формуле

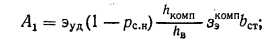
С учетом вышеизложенного в табл. 4 приведены примеры оптимизационных моделей водяных и паровых СЦТ. Из равенства нулю первых частных производных целевых функций можно получить формулы для вычисления в явном виде локально оптимальных значений отдельных параметров СЦТ при комбинированной схеме энергоснабжения:

Формулы для оптимальных значений параметров СЦТ

Анализ производных целевых функций оптимизационных моделей СЦТ свидетельствует о целесообразности применения аналитико-численных методов покоординатной оптимизации. Известно, что высокоэффективные по скорости сходимости алгоритмы минимизации являются сложными в практической реализации и требуют значительного объема вычислений на каждом шаге оптимизации. В то же время метод покоординатного спуска Гаусса — Зейделя, обладая значительно худшими теоретическими показателями скорости сходимости и требуя значительно большего числа шагов при заданной точности оптимизации, отличается простотой и позволяет находить минимум унимодальной функции.

Для описанных оптимизационных моделей СЦТ появляется возможность повышения точности нахождения минимума методом покоординатной оптимизации (релаксации) за счет того, что она проводится по большинству переменных по формулам в явном виде. Особенно важным является тот факт, что в данном случае не только линейные, но и выпуклые ограничения сводятся к простым относительно переменной, по которой осуществляется шаг покоординатной оптимизации. Естественно, что расчет минимального и максимального значений соответствующего параметра по всем ограничениям каждый раз должен предшествовать шагу оптимизации по этому параметру, который представляет собой минимизацию унимодальной функции на отрезке.

Для локализации минимума с заданной точностью (в случае невозможности его определения в явном виде) наиболее эффективным является использование принципов динамического программирования и последовательности Фибоначчи [4, 66]. Недостаток метода Фибоначчи заключается в необходимости априорного знания числа испытаний. От этого недостатка свободен метод золотого сечения, представляющий собой модификацию метода Фибоначчи. Этот метод основан на разбиении отрезка прямой на две части таким образом, что отношение длины отрезка к его большей части равно отношению большей и меньшей частей [66]. Для достижения точности 0,5 % необходимо произвести всего 12 испытаний по методу золотого сечения. Число вычислений Целевой функции в этом случае примерно в 3,4 раза меньше, чем по методу половинного деления.

Таким образом, для решения задачи комплексной оптимизации основных параметров СЦТ с помощью вышеописанных оптимизационных моделей в детерминированной постановке целесообразно применять метод покоординатной оптимизации с отбраковкой ограничений (метод проектирования на допустимую область).

Учет неопределенности исходной информации о значениях факторов можно производить с помощью методики составления и анализа платежной матрицы, изложенной в работах [30, 31, 48, 67, 68].

При перспективном проектировании перечисленные факторы для оптимизационных моделей СЦТ представляют собой частично неопределенную информацию, которая практически может быть задана некоторым отрезком «от и до». Примеры подобной информации приведены в работах [30, 68].

Как указывалось в гл. 1, выбор решения в условиях неопределенности наиболее убедителен по так называемым средним затратам, соответствующим гипотезе о равновероятности наиболее представительных сочетаний значений факторов в интервале их изменения [30, 31]. Поскольку факторы, принятые в постановке оптимизационной задачи, являются непрерывными, затрудняется обоснованный выбор их наиболее представительных сочетаний. С целью повышения точности расчетов необходимо увеличивать число представительных сочетаний факторов для составления и анализа платежной матрицы. В пределе получения среднее арифметическое затрат по строкам платежной матрицы будет стремиться к среднеинтегральной величине, что формально соответствует математическому ожиданию затрат при равномерном законе распределения факторов. Следовательно, в рассматриваемом частном случае исходная задача оптимизации определяющих параметров СЦТ при частично неопределенном характере факторов может быть условно сведена к задаче перспективного стохастического программирования в чистых стратегиях, так как решение представляет собой детерминированный вектор.

Специальный вид целевых функций для комплексной оптимизации основных параметров СЦТ позволяет свести решение задачи перспективного стохастического программирования в чистых стратегиях к однократному решению детерминированной задачи минимизации целевой функции, коэффициенты которой представляют собой математические ожидания функций факторов при равномерном законе их распределения. Докажем это в виде обобщения теоремы об эквивалентности форм, частный случай которой для специальной задачи линейного программирования описан без доказательства в работе [5].

Указанный методический прием позволит резко сократить объем вычислительной работы по сравнению с процедурой составления и анализа платежной матрицы и увеличить размерность задач, решаемых на практике.

Юфа А. И., Носулько Д. Р./ Комплексная оптимизация теплоснабжения.— К.: Техника, 1988.