СЕТЕВЫЕ МОДЕЛИ И ПОТОКОВЫЕ АЛГОРИТМЫ ОПТИМАЛЬНОГО СИНТЕЗА НАДЕЖНЫХ СИСТЕМ ЦЕНТРАЛИЗОВАННОГО ТЕПЛОСНАБЖЕНИЯ
При перспективном проектировании на достаточно отдаленный период возрастающая неопределенность условий развития и функционирования СЦТ приводит к целесообразности применения упрощенных оптимизационных математических моделей (в первую очередь, линейных и непрерывных). В отличие от рассмотренных в гл. 4 матричных постановок транспортных задач оптимизации структуры СЦТ, в данной главе рассматриваются сетевые модели синтеза оптимальной структуры СЦТ с учетом надежности.
В матричной постановке транспортных задач все возможные пути прохождения потоков от источников к потребителям необходимо установить до решения оптимизационной задачи для определения удельных транспортных затрат. При сетевой постановке вся исходная информация задается на дугах расчетной сети, а оптимальные пути прохождения потоков определяются решением зедачи. Матричная и сетевая постановки транспортной задачи эквивалентны: любая матричная задача может быть представлена в сетевой форме и наоборот. Однако сетевая постановка обладает рядом практических преимуществ.
В частности, в сетевой модели нет принципиальной разницы между источниками теплоты, узлами ветвления тепловых сетей и потребителями (в матричной постановке источники и потребители строго разделены), что существенно облегчает моделирование сложных СЦТ с несколькими источниками теплоты, разветвленными и закольцованными тепловыми сетями. Пользуясь однажды составленной расчетной схемой СЦТ, можно с ее помощью решать большое количество различных оптимизационных задач, незначительно корректируя первоначальную конфигурацию схемы и часть исходных данных.
Сетевая постановка обеспечивает экономное представление информации, сокращая трудоемкость подготовки исходных данных, объем машинной памяти и вычислительных операций и повышая скорость решения задач (практически всегда число дуг на сети намного меньше числа клеток соответствующей матрицы). Сетевая постановка позволяет легко учитывать ограничения на мощность источников и пропускную способность сетей. Поэтому рассмотрим подробнее именно сетевые постановки транспортных задач оптимизации, структуры СЦТ (выше была показана возможность сведения производственно-транспортных задач к транспортным) и потоковые алгоритмы их решения.
Наиболее общая динамическая модель синтеза оптимальной структуры СЦТ с учетом требований резервирования в сетевой постановке имеет вид г


Рассмотрим возможности сведения решения общей задачи (95) — (100) к решению последовательности более простых задач, для которых имеются эффективные методы оптимизации.
В частности возможна декомпозиция непрерывной многоэтапной динамической задачи на решение последовательности статических задач на каждом из интервалов расчетного периода [16]. Так как задача (95) — (100) является непрерывной при практически неубывающих потребностях в узлах сети, решение на каждом интервале определяет оптимальное развитие системы, а полученные конечные значения пропускных способностей дуг являются начальными значениями для следующего этапа расчетов. Таким образом исходная задача распадается на решение Т статических задач при фиксированном t, каждая из которых заключается в синтезе оптимального перехода системы в очередное состояние с учетом требований выполнения ограничений по резервированию:
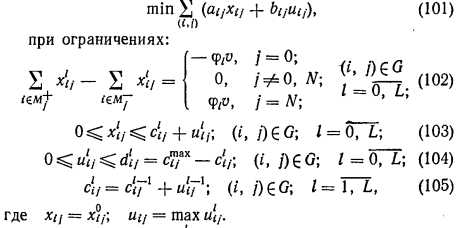
В свою очередь, решение статической задачи (101)— (105) также разбивается на решение последовательности однотипных (для каждого режима О, L — нормального, а затем аварийных в порядке убывания пропускной способности нагруженных в нормальном режиме дуг) задач об оптимальном преобразовании заданной сети вида
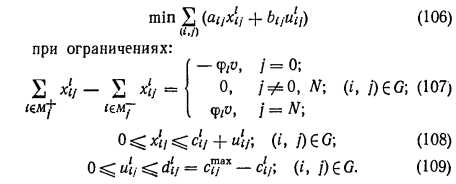
Задача минимизации кусочно-линейной выпуклой функции потока и приращений пропускной способности дуг сети вида (106)— (109) известна в литературе, а ее решение можно свести к решению классической линейной задачи о циркуляции минимальной стоимости, для которой имеются эффективные потоковые алгоритмы [18, 58, 62, 63, 69].
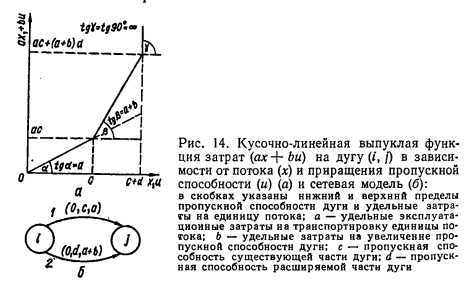
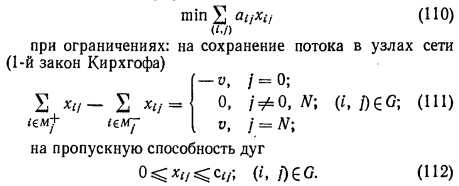
Рассмотрим краткую характеристику основных потоковых алгоритмов для решения задачи о циркуляции минимальной стоимости: Басакера—Гоуэна [18, 69], Клейна [58, 69], прямого базисного [18] и дефекта [18, 62, 63].
Алгоритм Басакера—Гоуэна (метод увеличения потока) выполняет последовательное наращивание потока через расчетную сеть до заданной величины, обеспечивая минимум стоимости при каждом значении потока. Метод состоит из двух итеративных шагов: определения кратчайшего (самого дешевого) пути из обобщенного источника в обобщенный сток, состоящего только из допустимых дуг, и увеличения потока вдоль найденного пути на максимально возможную величину. Изменение потока приводит к формированию новой ситуации в сети и происходит повторение первого шага. Процесс итераций продолжается до выключения одного из двух условий останова: если удовлетворена потребность в обобщенном стоке, то полученные дуговые потоки являются оптимальным решением задачи, а если потребность обобщенного стока еще не удовлетворена, но уже нельзя найти путь из обобщенного источника в обобщенный сток, то задача не имеет допустимого решения (заданный поток нельзя пропустить через расчетную сеть). Если величина максимального потока заранее неизвестна, то с помощью указанного алгоритма определяется максимальный поток минимальной стоимости.
Алгоритм Клейна базируется на теореме, согласно которой утверждается, что данный поток является потоком минимальной стоимости только тогда, когда в сети отсутствует цикл (конечный путь, начальный и конечный узлы которого совпадают) отрицательной стоимости.
Прямой базисный алгоритм является аналогом симплекс-метода, используемого при решении общей задачи линейного программирования. В работе [18], где приведено подробное описание данного алгоритма, подчеркивается его эффективность в вычислительном отношении.
Алгоритм дефекта является наиболее общим методом определения потока минимальной стоимости с учетом как верхних, так и нижних ограничений на пропускную способность дуг. Величина дефекта характеризует для каждой дуги степень невыполнения для нее условий оптимальности. Основная идея алгоритма дефекта состоит в последовательном уменьшении до нуля величины дефекта какой-либо дуги без увеличения величин дефектов остальных дуг. Алгоритм дефекта подробно описан в работах [18, 62, 63], а в приложении к книге [62] приведен текст стандартной программы на ФОРТРАНЕ, реализующей этот алгоритм.
Задача о циркуляции минимальной стоимости в сети вида (110) — (112) занимает главное место в потоковом программировании [18]. К рассмотренной динамической задаче синтеза оптимальной структуры СЦТ (с учетом требований резервирования) сводятся и другие задачи оптимизации СЦТ, имеющие большое практическое значение. Так, решение задачи о циркуляции минимальной стоимости позволяет определить оптимальное потокораспределение в сети, включая выбор зон охвата потребителей от различных источников и определение целесообразности постоянного (нагруженного) резервирования или резервирования замещением (ненагруженного), т. е. решить задачу анализа сети.
Так как задачи с кусочно-линейными выпуклыми функциями стоимости дуг можно решать путем сведения их к линейным задачам о циркуляции минимальной стоимости, то эти задачи можно рассматривать в качестве одного из возможных вариантов экстремального перехода к решению задач о потокораспределении в гидравлических сетях [18] (в частности, в водяных, тепловых) нахождением минимума энергетического функционала, являющегося кубической функцией расхода теплоносителя [33].
В отличие от наиболее широко распространенных алгебраических методов решения задач потокораспределения в гидравлических сетях [33, 35] потоковые алгоритмы позволяют легко учитывать ограничения на пропускную способность участков сетей в процессе решения задачи (например, по скорости теплоносителя не более 3,5 м/с). Однако конкурентоспособность потоковых алгоритмов по сравнению с алгебраическими методами нуждается в практической проверке, так как стремление к повышению точности расчетов увеличивает число параллельных дуг сети при кусочнолинейной аппроксимации, повышая размерность задачи и время счета на ЭВМ.
Важной практической задачей функционирования СЦТ является оптимальное распределение дефицита мощности источников и пропускной способности сетей в аварийных ситуациях. С точки зрения энергоснабжающей организации эта задача заключается в том, что при обеспечении ср %-ных норм для потребителей жилищно-коммунального сектора (ЖКС) необходимо минимизировать размер штрафа по 4-кратному тарифу за недоотпуск теплоты промышленным потребителям во время ликвидации аварии, т. е. передать максимум тепловой мощности, не задействованной для ЖКС, промышленным предприятиям без превышаения их потребности. Эта проблема формализуется в виде задачи о максимальном потоке минимальной стоимости, решение которой сводится к последовательному решению серии задач о потоке минимальной стоимости с возрастающей величиной потока до тех пор, пока не будет установлено, что дальнейшее увеличение потока через сеть невозможно. В частности, на такой идее базируется известный алгоритм Басакера — Гоуэна [58, 69]. В описанной задаче р %-ные ограничения для потребителей ЖКС задаются жестко, а для промышленных потребителей — 0 ср 1 (узлы сети, в которые входят потребители обоих видов, условно разбиваются на соответствующую пару узлов).
Максимизация потока через расчетную сеть при его минимальной стоимости позволяет находить оптимальные варианты использования резервов мощности источников и пропускных способностей сетей, а также минимизировать ущерб энергоснабжающей организации в виде штрафов за недоотпуск теплоты промышленным потребителям. При наличии оценок вероятного времени восстановления теплоснабжения при авариях элементов источников теплоты и участков тепловых сетей [10] можно дать количественную оценку математического ожидания ущерба энергоснабжающей организации при авариях, руб./год,
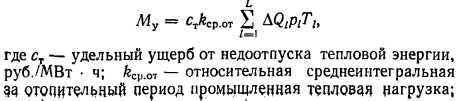

Учет математического ожидания ущерба в качестве слагаемого целевой функции в задаче синтеза оптимальной структуры СЦТ существенно увеличивает объем расчетов при оптимизации, так как в этом случае для любого варианта структуры в каждом интервале расчетного периода необходимо для всех аварийных режимов решать задачу о максимальном потоке минимальной стоимости. По-видимому, для решения задачи синтеза оптимальной структуры СЦТ с учетом ущерба необходима диалоговая процедура оптимизации (решение задач оптимального синтеза структуры СЦТ с учетом ограничений резервирования и оптимального распределения дефицита мощности источников и пропускной способности сетей с помощью оптимизационных моделей при задании человеком различных вариантов дополнительного усиления пропускных способностей дуг сети с расчетом дополнительных затрат на резервирование и определением математического ожидания ущерба).
В результате решения линейной динамической задачи синтеза оптимальной структуры СЦТ можно получить кусочно-линейные эпюры оптимального развития отдельных элементов системы, которые служат основой для выбора соответствующих дискретных вариантов. Учет дискретности основного оборудования источников теплоты и диаметров трубопроводов тепловых сетей возможен в рамках описанных выше производственно-транспортных моделей частично целочисленного программирования.
Значительные размерности подобных задач приводят к необходимости их декомпозиции на целочисленную задачу синтеза структуры системы и непрерывную задачу анализа с целью нахождения оптимального потокораспределения (циркуляции минимальной стоимости) [6]. Это легло в основу разработанного в лаборатории трубопроводных систем СЭИ СО АН СССР метода многоконтурной оптимизации (33, 57], реализованного в программно-вычислительном комплексе (ПВК) СОСНА. ПВК СОСНА позволяет решать статическую задачу оптимального синтеза трубопроводных (в частности, тепловых) сетей с учетом узловых норм надежности путем поочередной оптимизации диаметров трубопроводов тепловых сетей при заданном потокораспределении с помощью программы DIPR [19, 35] и нахождения потокораспределения в заданной сети с помощью программы АСИГР (35] до совпадения расходов теплоносителя на участках сети на соседних итерациях [33, 57]. Достоинством ПВК СОСНА является возможность учета дискретности диаметров трубопроводов и возможностей реконструкции тепловых сетей, выбора мест установки и параметров насосных станций, рельефа местности и 2-го закона Кирхгофа при решении задачи потокораспределения. Такое усложнение задачи, увеличивая потребные ресурсы памяти и быстродействия ЭВМ, все же приводит к возрастанию времени счета, что затрудняет непосредственное использование комплекса в диалоговом режиме.
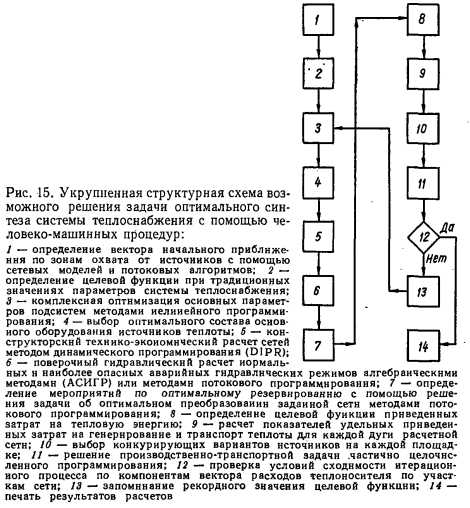
На рис. 15 изображена укрупненная структурная схема возможного решения задачи синтеза оптимального развития и функционирования СЦТ на базе многометодной оптимизации (совместного использования методов потокового, линейного целочисленного, нелинейного, динамического программирования, а также алгебраических методов расчета стационарного потокораспределения).
Юфа А. И., Носулько Д. Р./ Комплексная оптимизация теплоснабжения.— К.: Техника, 1988.
