ТРАНСПОРТНЫЕ МОДЕЛИ ОПТИМАЛЬНОГО ПЛАНИРОВАНИЯ ТЕПЛОСНАБЖЕНИЯ

Многие постановки производственно-транспортных задач путем преобразований сводятся к решению транспортных задач (например, путем введения обобщенного источника и фиктивных транспортных связей его с фактическими источниками). Для транспортных задач (особенно линейных) разработаны эффективные вычислительные алгоритмы, существенно использующие их специфику и позволяющие достаточно оперативно решать задачи большой размерности [9, 18, 23, 62, 63, 69]. Во многих случаях незначительная модификация методов решения транспортных задач позволяет решать широкий класс специальных задач (в первую очередь, линейного программирования), которые называются задачами транспортного типа [9].

Классическая транспортная задача решает проблему экономичного плана транспорта однородных или взаимозаменяемых продуктов из пунктов производства (источников теплоты) в пункты потребления (абонентские установки потребителей теплоты). Применительно к СЦТ эту задачу можно сформулировать следующим обазом. Имеется т источников теплоты и п ее потребителей. Заданы тепловые мощности а, каждого источника теплоты и потребности; каждого потребителя, а также удельные приведенные затраты (или эксплуатационные расходы) на транспорт единицы тепловой мощности от i-ro источника к-му потребителю сц. Требуется определить потоки тепловой мощности

Практически же почти всегда суммарная мощность источников теплоты должна несколько превышать суммарную тепловую нагрузку (например, по условиям дискретности основного оборудования источников, требованиям резервирования). Поэтому баланс производства и потребления тепловой энергии нарушается и условия равенства (63) заменяются ограничениями-неравенствами:

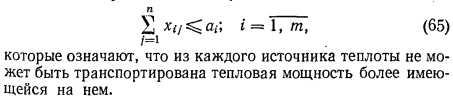
Полученная задача минимизации целевой функции (61) при условиях (62), (65) и (64) называется открытой транспортной моделью [9]. Эта модель сводится к замкнутой путем введения фиктивного (п + 1)-го потребителя с тепловой нагрузкой, равной разности между суммарной тепловой мощностью источников и суммарной тепловой нагрузкой

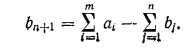
Недоиспользованные тепловые мощности источников можно оптимизировать в зависимости от введенного штрафа С(,га+1 за единицу незагруженной тепловой мощности i-го источника. Рассмотрим примеры возможных постановок задач оптимального планирования теплоснабжения в терминах задач линейного программирования транспортного типа. Простейшая модель — это использование известной задачи о назначениях для оптимального распределения основного оборудования источников теплоты (i = 1, п) по объектам их строительства вида

Условия (66) означают, что каждая i-я единица основного оборудования, намеченная к производству, должна быть использована. Условия (67) означают, что каждый объект строительства СЦТ должен быть обеспечен основным оборудованием источников теплоты. Для решения задачи о назначениях могут быть использованы эффективные алгоритмы решения транспортной задачи, например, метод потенциалов, венгерский метод и др. [9].

Юфа А. И., Носулько Д. Р./ Комплексная оптимизация теплоснабжения.— К.: Техника, 1988.