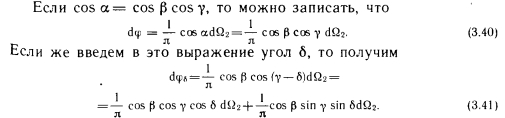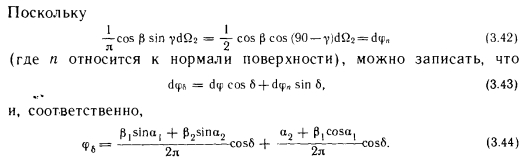Определение коэффициента облученности между поверхностью и элементарной площадкой путем расчета
На практике коэффициент облученности довольно редко определяют расчетным путем, поскольку для этого приходится пользоваться весьма сложными зависимостями, что затруднительно при проведении расчета «вручную».
Как исходный случай определим коэффициент облученности между плоскостью призмы с ребрами aXbXh и элементарной площадкой, расположенной перпендикулярно ей на расстоянии h.
Интегрирование части основного уравнения лучистого теплообмена (3.1), выражающей коэффициент облученности, дает следующую зависимость:
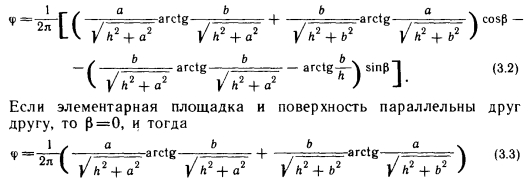
Если элементарная площадка расположена в плоскости, перпендикулярной поверхности, т. е. J=90°, то различают два случая. В первом случае поверхность находится в плоскости, ограничиваемой ребром а, и тогда
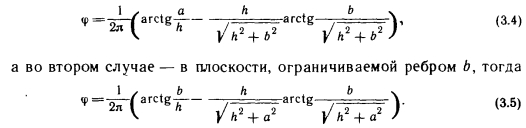
Следует заметить, что зависимости (3.2), (3.3) и (3.5) касаются только особых случаев, когда рассматриваемая элементарная площадка расположена на расстоянии h от плоскости, считающейся излучающей поверхностью, однако во всех случаях непосредственно у какой-либо угловой точки.
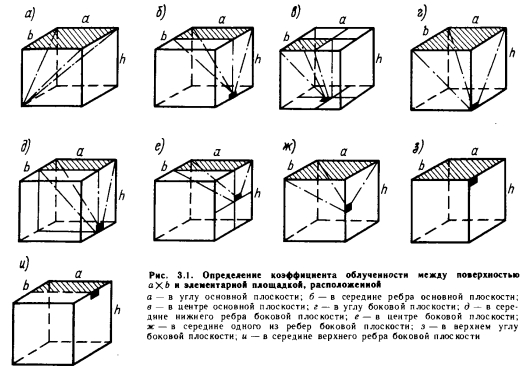
Рассмотрим варианты расчета коэффициентов облученности для различных точек (элементарных площадок) кубообразного помещения, используя соответствующие зависимости.
Первый случай. В теплообмене участвуют поверхность (aXb) и элементарная площадка, расположенная в углу основной плоскости (рис. 3.1, а). Пусть a = b =h= 1, тогда из уравнения (3.3) имеем
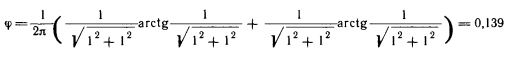
Второй случай. Пусть элементарная площадка будет расположена у середины ребра, ограничивающего основную плоскость (рис. 3.1, б). Здесь можно считать, что элементарная площадка относится к двум призмам размером aX(b/2)Xh и поэтому доля лучей, поступающих с потолка на элементарную площадку, будет вдвое больше, чем для одной призмы, т. е.
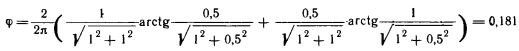
Третий случай. Элементарная площадка находится в центре основной плоскости (рис. 3.1, в). Можно рассматривать четыре призмы, ребра которых а/2= Ь/2 = 0,5, а высота h= 1, поэтому
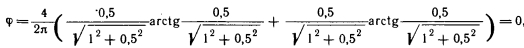
Четвертый случай. Элементарная площадка расположена в углу боковой плоскости. При этом
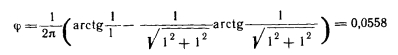
Пятый случай. Элементарная площадка находится на середине нижнего ребра боковой плоскости. Здесь
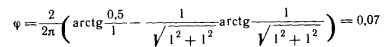
Шестой случай. Элементарная площадка расположена в центре боковой плоскости. В данном случае
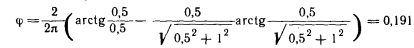
Седьмой случай. Элементарная площадка находится в середине одного из ребер боковой плоскости (рис. 3.1, ж); a~b= 1; Н/2 = 0,5. Здесь
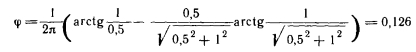
Если элементарная площадка находится на верхнем ребре боковой плоскости в углу [восьмой случай (рис. 3.1, з) ] или в середине [девятый случай (рис. 3.1, и) ], то зависимость (3.4) не имеет смысла, поскольку знаменатель первого члена Л = 0.
Если элементарная площадка dAi находится под осью симметрии какой-либо поверхности площадью Л2 = 2а X26 = 4ай на расстоянии h и Ьфа (рис. 3.2), то
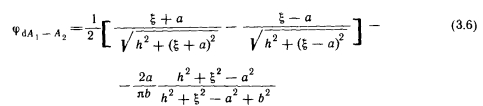
Эту зависимость можно использовать для расчета отопления одноэтажного промышленного здания, обогреваемого отопительными экранами, или для расчета потолочного отопления.
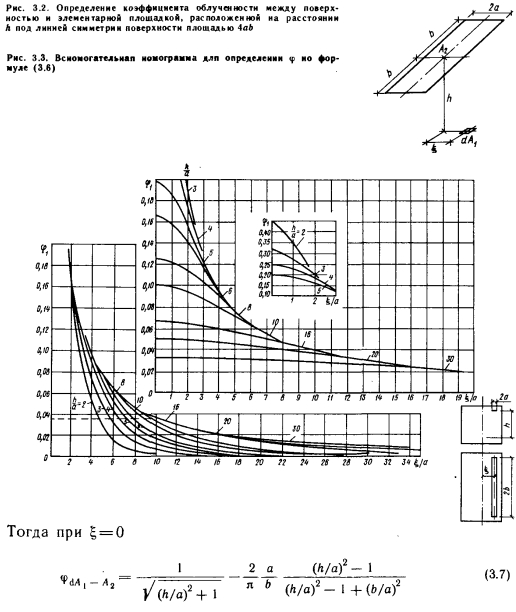
Для быстрого вычисления по зависимости (3.6) предназначены номограммы, приведенные на рис. 3.3 и 3.4. Номограмма на рис. 3.3 служит для вычисления — члена, заключенного в квадратные скобки, фи а номограмма на рис. 3.4 — для вычисления второго члена ф2.
Эти номограммы без каких-либо ограничений могут быть использованы и для случая, когда ? = 0. При этом величина ф: на рис. 3.3 может быть определена по ординате /а = 0, а параметр (h2-f-2)/a2 принимает вид h2/a2 в номограмме, применяемой для определения фг (см. рис. 3.4).
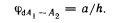
На рис. 3.5 приведена схема, а на рис. 3.6 — номограммы для определения коэффициента облученности квадратными нагревателями. Часто для вычислений используется принцип суммирования или вычитания коэффициентов облученности (рис. 3.7), при этом
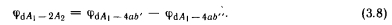
Наконец, хорошее приближение для эмпирического определения значения ф в случае крупных одноэтажных промышленных зданий, которые имеют совокупность экранов, расположенных под потолком, дает зависимость
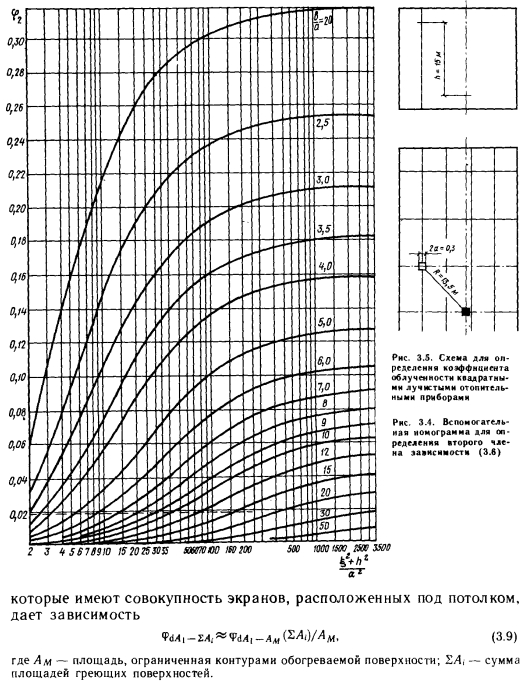
Подобному принципу можно следовать в том случае, если требуется вычислить коэффициент облученности поверхности площадью А1 совокупностью лучистых нагревателей, расположенных на поверхности площадью А?.
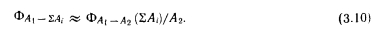
Общий случай, когда элементарная площадка и поверхность расположены в плоскостях параллельных, но смещенных относительно друг друга, д-р Золтан Мольнар на основании лекций доктора А. Мачкаши рассматривает следующим образом.
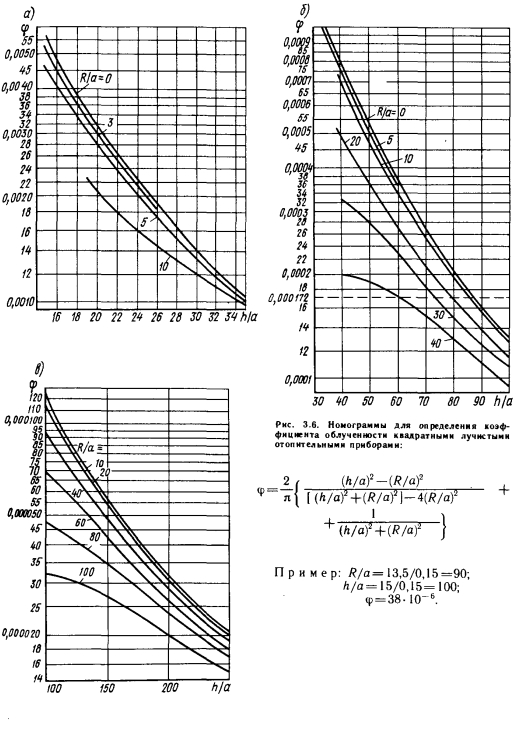
Для общего случая, представленного на рис. 3.8, коэффициент облученности может быть вычислен по формуле

Особый случай выражения (3.11) дает зависимость (3.3).
При некоторых конструкциях излучающей поверхности размеры поверхности Л2 (отопительный прибор) могут на несколько порядков отличаться от других геометрических размеров. Например, при отоплении экранными излучателями узкие длинные излучатели обычно располагают на большой высоте, при этом Ь>а и а<С/г. Полагая г) = 0, можно найти значение коэффициента облученности для наиболее неблагоприятного случая. В этом случае с очень хорошим приближением можно пользоваться следующей зависимостью:

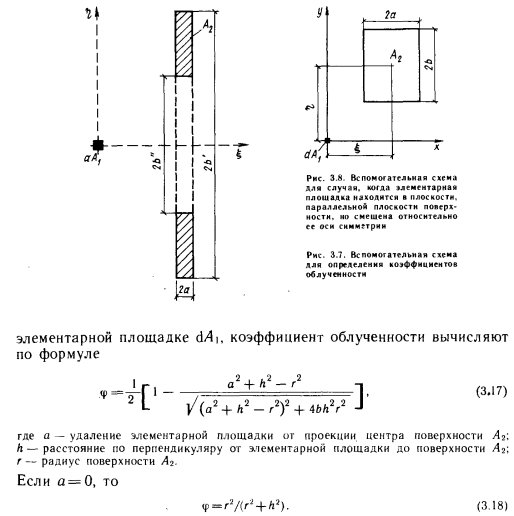
Подробно коэффициентом облученности занимался Э. Эккерт [40]. Многие разработанные им методы усовершенствованы, но некоторые его решения, касающиеся рассматриваемого ниже особого случая, действительны без изменений. Изложим сначала основные принципы метода Эккерта.
Рассмотрим излучение, идущее с элементарной площадки dA (рис. 3.10). Используя известные общие закономерности, можно описать его следующей зависимостью:
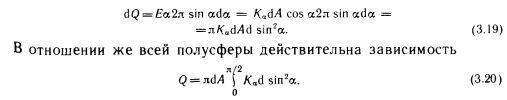

Коэффициент облученности элементарной площадки (для излучения с элементарной площадки на элементарную площадку 2) при этом можно определить по зависимости

После интегрирования получим коэффициент облученности с элементарной площадки d/li на всю поверхность 2, выраженный зависимостью

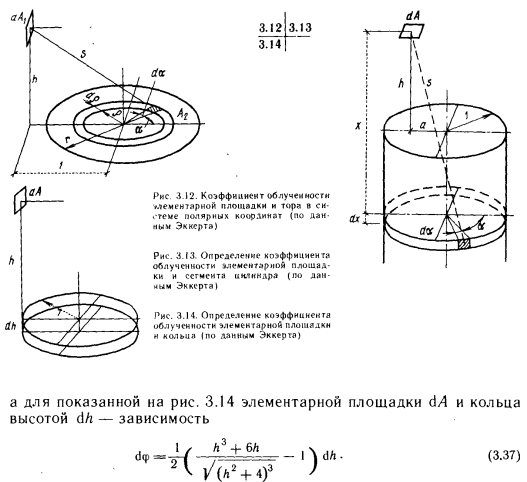
Рассмотрим два решения, в которых использованы закономерности начертательной геометрии. Одно из них представлено на рис. 3.15, где показан лучистый теплообмен между элементарной площадкой АА и параллельной ей поверхностью. В конечном итоге (если пренебречь подробностями, поскольку к теоретическим основам мы вернемся при рассмотрении графических решений) получаем:

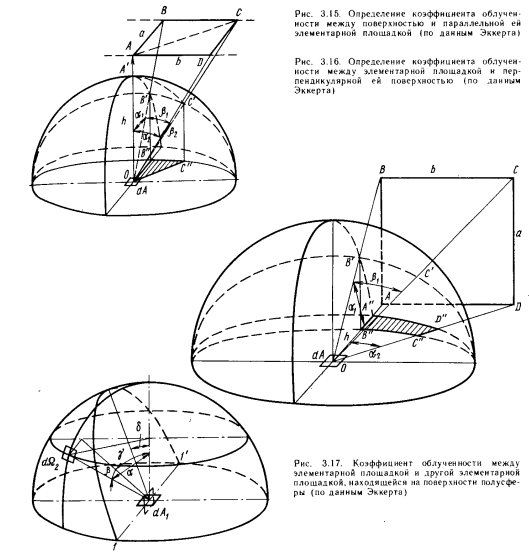
Рассмотренные выше рисунки 3.15 и 3.16 и зависимости (3.38) и (3.39) несколько противоречат данным, представленным в п. 3.2, но мы сочли необходимым изложить этот материал, поскольку он позволяет расширить наши знания о коэффициентах облученности.
Случай же, показанный на рис. 3.17, до сих пор не рассматривался. Ход рассуждений здесь следующий.