ПОСТАНОВКА И МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ ОПТИМИЗАЦИИ ПАРАМЕТРОВ ТЕПЛОВЫХ СЕТЕЙ
В настоящее время в практике проектных организаций полечили широкое распространение упрощенные методы расчета водяных тепловых сетей, при которых схема сети и размещение подкачивающих и дросселирующих подстанций намечаются без оптимизационных расчетов, а диаметры трубопроводов определяются по нормативному значению удельной линейной потери давления— до 78,5 Па/м (до 8 мм вод. ст/м), принимаемой постоянной по направлению главной магистрали. При этом места расположения и параметры подкачивающих и дросселирующих подстанций выбираются на основе инженерной интуиции и опыта проектировщика. Эти методы базируются на фундаментальных исследованиях аналитических методов оптимизации параметров тепловых сетей, выполненных проф. Б. Л. Шифринсоном еще в 30-х годах [76] и впоследствии развитых в трудах других энергетиков [14, 28, 43, 60]; они обеспечивали принятие в достаточной степени оптимальных решений при проектировании тепловых сетей на первых этапах развития систем централизованного теплоснабжения, когда эти системы были сравнительно небольшими. Такие упрощенные методы расчета тепловых сетей могут применяться и в настоящее время при проектировании сравнительно мелких систем теплоснабжения с незначительной протяженностью тепловых сетей. В то же время они не могли в полной мере использовать теоретические положения этих исследований ввиду ограниченных возможностей ручного счета. Зачастую при сравнении комбинированной и раздельной схем энергоснабжения городов и промышленных центров затраты в тепловые сети определяются на основе обобщенных зависимостей капиталовложений в тепловые сети от укрупненных показателей теплоплотности теплофицируемых районов. При использовании таких методов не учитываются постепенность роста тепловых нагрузок потребителей по годам расчетного периода, наличие существующих участков сети и не оптимизируются диаметры по участкам тепловых сетей с учетом технических ограничений на давления в узловых точках сети, различных удельных капиталовложений по ее участкам, что может приводить к существенным просчетам и ошибкам. Применение ЭВМ открывает большие возможности для создания новых, более совершенных и точных методов оптимизации развития тепловых сетей [26, 41, 42, 50, 65].
Задача оптимизации тепловых сетей может решаться как без учета, так и при учете постепенности роста тепловых нагрузок по годам расчетного периода. В случае, если фактор динамики не учитывается, постановка задачи может быть сформулирована следующим образом. Задано: расчетные расходы воды у потребителей; длина участков и конфигурация тепловой сети; область допустимых значений удельного падения напора в главной магистрали; срок службы существующей тепловой сети и диаметры по ее отдельным участкам; шкала стандартов возможных диаметров тепловой сети; допустимый располагаемый напор на вводе у абонентов; технические ограничения на давление в узловых точках сети. Требуется определить: оптимальные значения диаметров по участкам сети; количество, места расположения и параметры подкачивающих и дросселирующих подстанций, соответствующие минимальному значению целевой функции, в качестве которой принимаются приведенные затраты в тепловую сеть Входящие в величину капиталовложения /Ст.с вычисляются по формуле:
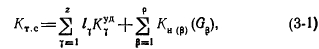

Оптимизация параметров тепловой сети, т. е. нахождение минимума функции приведенных затрат с применением математического моделирования и ЭВМ, может выполняться следующими методами:
1) перебор достаточно большого числа вариантов с различными значениями удельного падения давления по направлению главной магистрали при условии линейного закона падения давления по этому направлению (линейный метод);
2) метод, основанный на применении динамического программирования (нелинейный метод).
В общем виде математическая постановка задачи оптимизации тепловой сети при использовании линейного метода может быть записана так. Найти:

Линейный метод оптимизации тепловой сети заключается в полном переборе заданных значений удельного падения напора (h) в главной магистрали сети, принимаемого одинаковым на всех ее участках, и в нахождении его оптимальной величины, соответствующей минимуму критериальной функции. При вычислении /г(ШТ необходимость перебора всех его значений (с заданным шагом), лежащих в допустимой области, вызывается тем, что зависимость 3=f(h) не характеризуется строгой плавной монотонностью, т. е. могут иметь место локальные минимумы. Возможность их появления вызывается дискретностью диаметров труб и типоразмеров строительных конструкций, а также наличием участков в развивающихся тепловых сетях. При этом локальные минимумы будут соответствовать тем вариантам, при которых существующие участки не перекладываются. При применении этого метода в результате расчета на ЭВМ можно получить не один оптимальный вариант, а набор ряда вариантов, незначительно отличающихся от оптимального по приведенным затратам. Это позволяет проектировщику выбрать вариант не только по формальному критерию минимума приведенных затрат, но и с учетом эксплуатационных требований, например гидравлической устойчивости и надежности.
Допущение о линейности закона падения напора вдоль главной тепломагистрали упрощает расчет тепловой сети и в то же время вносит погрешность в результаты ее оптимизации. Например, линейный метод не позволяет в полной мере учесть различия в способах прокладки трубопроводов для разных участков сети. В случае оптимизации развивающейся сети с существующими участками такой метод не позволяет учесть важную особенность, заключающуюся в том, что для новых участков сети оптимальные значения удельной потери давления, как правило, меньше, чем для существующих. Это объясняется тем, что в сетях с существующими участками больше доля затрат на перекачку теплоносителя в суммарных затратах по тепловой сети.
Нелинейный метод оптимизации тепловых сетей основан на разделении главной магистрали сети на отдельные участки с пошаговой оптимизацией сети по отдельным участкам [26]. При этом методе вместо нахождения минимума функции приведенных затрат по всей сети, зависящих от диаметров всех участков, что требует решения сложной системы уравнений, последовательно находятся оптимальные решения для отдельных участков сети.
Основные исходные положения метода динамического программирования и последовательность решения задачи при его применении выше рассмотрены на примере оптимизации состава и сроков ввода оборудования ТЭЦ. В данном случае пошаговый процесс строится с учетом особенностей задачи оптимизации тепловой сети. За основу (фазовую переменную) принимается напор, который разбивается на ряд значений (в заданных пределах— от минимального до максимально допустимого значения), образующих узлы решетки. При переборе вариантов на каждом шаге и вычислении приведенных затрат для данного i-го напора Я, значение Я, приводится в соответствие с ближайшим стандартным диаметром. Пошаговый процесс оптимизации, принципиальную последовательность применения которого поясняют построения рис. 3-1 [26], начинается с последнего участка у, так как напор в конце сети предполагается известным. При этом рассматриваются все возможные решения для данного участка, соответствующие стандартным значениям диаметра. Решения, при которых напор в начальном узле рассматриваемого участка выходит за пределы допустимого диапазона, в дальнейшем не учитываются. Если в один узел решетки попадает несколько значений диаметра, то по критерию минимума приведенных затрат определяется оптимальное решение для этого узла
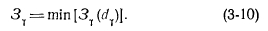
На следующем шаге учитываются в расчетах два участка — последний у и предпоследний (у—1), при этом рассматриваются возможные решения для участка (у—1), являющиеся продолжением оптимальных решений для каждого узла решетки, полученных на предыдущем шаге. Если в один узел решетки попадает несколько решений (вероятность этого значительно больше, чем на первом шаге), то определяется оптимальное решение для двух участков у и (у—1):
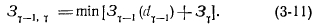
Путем добавления к уже рассмотренным очередного (в порядке расположения) участка тепловой сети процесс оптимизации повторяется. Таким образом, на каждом шаге в качестве фазовой переменной, по которой производится оптимизация, принимается диаметр начального участка оптимизируемой части сети. При этом число возможных решений, фиксированных для данного шага, при переходе к следующему шагу (участку тепловой сети), как правило, меньше числа узлов решетки, х. е. числа заданных значений напора в сети, которое остается одним и тем же в течение всего пошагового процесса оптимизации. Окончательное решение в целом по сети выбирается после завершения этого процесса и сравнения между собой по величине суммарных приведенных затрат всех полученных «траекторий», т. е. возможных вариантов, число которых не превышает заданного числа значений напора в сети. Обоснованность применения динамического программирования для оптимизации тепловых сетей показана в [26].
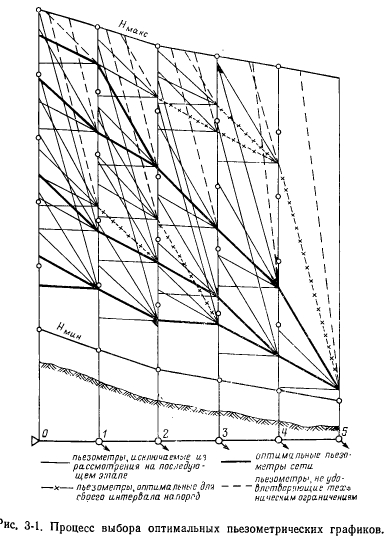
Нелинейный метод оптимизации позволяет учесть технические и стоимостные характеристики каждого участка сети, выбирать оптимальные места сооружения и параметры насосных подстанций, оптимизировать развивающиеся сети с существующими участками. Этот метод, основанный на пошаговой оптимизации, применим для разветвленных сетей как с одним, так и с несколькими источниками тепла, по но может быть использован для оптимизации кольцевых сетей, так как в этих сетях в зависимости от диаметра на одном из участков меняются расходы воды на других участках сети. Как нелинейный, так и линейный методы оптимизации могут быть применены для кольцевых сетей только в тех случаях, когда с допустимой погрешностью кольцевая сеть может быть преобразована в радиальную и предварительно задано в ней потокораспределение.
Для оценки сравнительной эффективности различных методов оптимизации производились расчеты тепловых сетей разной конфигурации тремя методами: методом, широко распространенным в настоящее время в проектной практике и основанным на использовании нормативов и ручного счета (а); методом оптимизации, основанным на предпосылке о целесообразности изменения напора в главной магистрали по линейному закону («линейный метод») при выполнении расчетов на ЭВМ (б); методом оптимизации на основе динамического программирования («нелинейный метод») при выполнении расчетов на ЭВМ (в).
