Основы статических и динамических расчетов

Одним из наиболее характерных факторов, существенно усложняющих задачу расчета и проектирования рассматриваемых сооружений, являются их большие габариты наряду с относительной близостью расположения смежных выработок. Первое обстоятельство обуславливает необходимость поярусной разработки пространства камер и их крепления, второе - практически исключает возможность их рассмотрения как одиночных выработок.

Важным следствием больших габаритов выработок является значительное увеличение по сравнению с туннелями глубины зоны разуплотнения массива. Именно этим объясняется прежде всего существенное изменение характера взаимодействия элементов системы массив-крепь: уменьшается роль крепи в непосредственном восприятии нагрузки на указанную систему и, наоборот, возрастает ее консолидирующее влияние на структурные элементы массива в зоне разуплотнения. Иначе говоря, НДС сооружений определяется главным образом физико-механическими и структурными параметрами массива. По этой причине при их математическом моделировании акцент (по сравнению с туннельными выработками) переносится с крепи на массив, что обуславливает определяющую роль Метода механики сплошных и дискретных сред.

В связи с изложенным выше существенно возрастает значение Фактора технологии строительства. Напряженное состояние конструкций крепей выработок в значительной мере определяется последовательностью строительных работ. Моделирование этой последовательности при расчетных исследованиях приводит к необходимости рассмотрения сложных многоэтапных СНРС таких сооружений.

Следующая важная особенность рассматриваемых строительных объектов заключается в том, что комплекс взаимосвязанных камерных и туннельных выработок, входящих в состав основных со- оружений подземного машинного зала ГЭС, в строгой постановке определяет сугубо пространственный характер задачи их расчета. Однако на сегодня достаточно корректная реализация подобной постановки в подавляющем большинстве практических случаев нереальна и, как правило, нецелесообразна в силу ряда существенных причин: низкий уровень достоверности инженерно-геологического описания грунтового массива; слабое развитие и техническое оснащение промышленных методик полевых изысканий; сложность описания в трехмерных расчетных схемах макроструктуры массива, конфигурации подземных выработок и технологической последовательности их проходки и крепления.

В силу указанных причин расчетные исследования реальных объектов выполняются в настоящее время, как правило, на базе плоских моделей. В известной степени такой подход оправдан протяженным характером самих камерных выработок - машинных залов и помещений трансформаторов. В результате задача их расчета, так же как и для туннелей, сводится к последовательному рассмотрению характерных поперечных сечений. При этом ослабление массива регулярной системой поперечных туннельных выработок (подводящих и отводящих водоводов и др.) учитывается в плоской расчетной схеме путем понижения значений характеристик его свойств в пределах площади их проекций на рассматриваемое сечение (рис. 4.13).

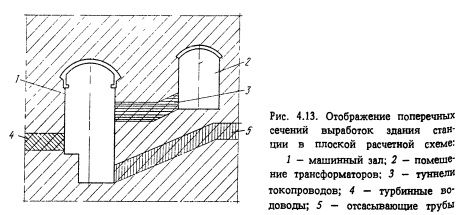
При рассмотрении каждого из возможных предельных состояний нормы (21] регламентируют следующий порядок расчетного обоснования крепей камерных выработок. Сначала на базе моделей механики сплошной среды определяется НДС массива и элементов конструкций крепи (железобетонной обделки, глубоких анкеров и др.). При этом определяются также конфигурации зон неупругих деформаций массива вокруг выработок. Затем выполняется проверка устойчивости контура выработок путем рассмотрения схем предельного равновесия всех потенциально неустойчивых грунтовых блоков (вывалов в своде, стеновых призм обрушения), оцениваемых в пределах вычисленных ранее зон неупругих деформаций. По наиболее неблагоприятным неустойчивым грунтоЕым блокам определяются геометрические и статические параметры крепи, обеспечивающие ее необходимую несущую способность при восприятии нагрузок расчетных комбинаций.

В настоящее время наиболее широкое применение при математическом моделировании подземных сооружений находят различные численные методы. Среди них наиболее универсальными возможностями для описания всех морфологических особенностей СНРС подземных сооружений обладает МКЭ.

Реализация конечноэлементной расчетной методики начинается с процедуры дискретизации расчетной области. При этом границы области принимаются достаточно удаленными от выработок, чтобы вызываемые ими возмущения в поле искомых функций с приближением к ним затухали. Для затухания перемещений точек массива, вызванных раскрытием сечения выработок, границы области должны быть удалены от нее на L = 25 В (где В - характерный размер выработки). Для обеспечения затухания возмущений функций напряжений достаточно принять.

Дискретный характер расчетных схем МКЭ позволяет легко моделировать массив неоднородной макроструктуры, включающей участки с различными физико-механическими свойствами, отдельные тектонические нарушения в виде разломов, крупных трещин, а также систем трещин различных порядков, обуславливающих блоч- ность массива. Контактные условия на границах указанных дискретных факторов могут моделироваться как с помощью объемных (плоских), так и специальных контактных элементов (типа элемента Гудмана).

Конструкции крепей выработок в зависимости от их характера могут представляться в дискретной модели как континуальными, так и дискретными (одномерными) КЭ. Так, в частности, в зависимости от относительной толщины обделки выработок могут аппроксимироваться многослойным набором объемных (плоских) КЭ, оболочеч- ными и стержневыми КЭ. Анкерные элементы крепи представляются в дискретной модели стержневыми КЭ, при этом характер их дискретизации определяется условиями контакта анкерного тяжа с массивом. При наличии сцепления по всей длине анкера он аппроксимируется непрерывной последовательностью стержневых КЭ, при отсутствии такового анкер моделируется одним стержневым КЭ, соединяющим точки его закрепления.

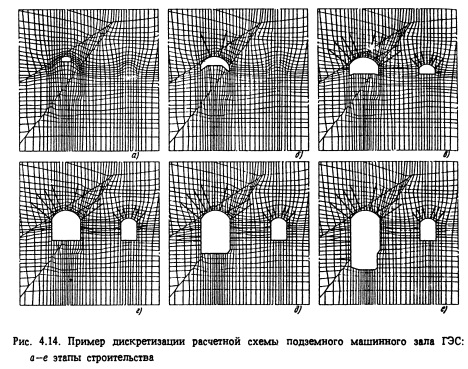
На рис. 4.14 приведен пример дискретной модели СНРС подземного машинного зала ГЭС.

Задачи стационарной напорной фильтрации и теплопроводности. Указанные задачи для рассматриваемых подземных сооружений чрезвычайно актуальны. Фильтрационные воздействия на них являются скорее правилом, нежели исключением. В большинстве случаев выработки проходятся и эксплуатируются в обводненных массивах. Изменение теплового режима вокруг выработок, располагаемых в вечномерзлых массивах, - определяющий фактор характера и интенсивности проявления горного давления на конструкции крепей в этих условиях. Как и в задачах статики, здесь в общем случае также необходимо моделировать в расчетных схемах характерные этапы строительства сооружения, т.е. рассматривать их как структурно-нелинейные системы.

Основной целью решения рассматриваемых задач является определение дополнительных нагрузок на подземные сооружения в процессе их строительства и эксплуатации, обусловленных гидродинамическим и гидростатическим воздействиями подземных вод, изменением температурного поля вокруг выработок.

Вследствие больших габаритов рассматриваемых камерных выработок снижение указанных воздействий на них является чрезвычайно важной задачей, решаемой с помощью специальных инженерных систем (дренажных, холодильных). Для оценки эффективности работы этих систем и определения на этой основе их рациональных параметров необходимо моделировать такие элементы в расчетных схемах сооружений. В математической постановке это означает необходимость учета в разрешающих соотношениях соответствующих краевых задач не только регулярных, но и дискретных членов, описывающих разрывной характер области и наличие в ней сингулярных факторов.

Расчетные параметры в плоской задаче задаются приведенными на единицу длины выработки в направлении, нормальном расчетному сечению, т.е. параметры соответствующих конструктивных элементов (дрен, тепловодов) делятся на шаг их установки в указанном направлении.

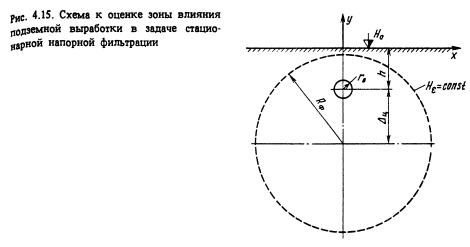
Для назначения границ расчетной области при численной реализации задач необходимо иметь оценку размеров зоны влияния выработок в стационарном поле. Приближенную оценку можно получить из рассмотрения единичной круговой выработки радиусом гв, расположенной на глубине h от дневной поверхности, на которой задано значение напора (рис. 4.15).

Решение физически нелинейных задач. Решения, получаемые на базе описанных выше линейно-упругих схем применительно к камерным выработкам, можно рассматривать лишь как начальное приближение. Количественное выражение таких сложных геологических явлений в грунтовом массиве, как пластичность, ползучесть и другие, для крупногабаритных выработок весьма существенно, поэтому нормы [21] определяют необходимость выполнения расчетов при оценке НДС на заключительных стадиях проектирования только на основе физически нелинейных моделей. Вместе с тем при обеспечении своевременного крепления раскрываемых участков выработок перемещения точек массива скальных грунтов остаются обычно достаточно малыми, чтобы можно было пренебречь нелинейностью связи между ними и деформациями и рассматривать задачу как геометрически линейную. В такой постановке нелинейную зависимость между напряжениями и деформациями можно учесть на основе общих вариационных принципов.

Решение таких задач, называемых физически нелинейными, строится в виде итерационной схемы, где нулевым приближением является упругое решение.

В отличие от метода переменных параметров в данном случае процедура вычисления матрицы [К] на итерациях заменяется на существенно более простую - вычисление нового грузового вектора. Однако такое существенное упрощение вычислений на итерациях вызывает ухудшение сходимости решения.

Решение, представленное в виде приращений, получило название метода начальных напряжений; при варьировании параметра метод начальных деформаций.

Поскольку в нелинейных задачах в отличие от линейных нет единственности решения для получения более точных результатов, рекомендуется применять метод малых приращений. Для ускорения сходимости итерационного процесса используются различные способы, основанные как на формально математических преобразованиях, так и учитывающих физическую природу задачи Г71.

При реализации физически нелинейных моделей фундаментальным является вопрос о выборе теории прочности и построении соответствующего критерия. В проектировании подземных сооружений получила широкое распространение теория прочности Мора. Обеспечивая в большинстве случаев удовлетворительную для практики точность (адекватную существующему уровню оценки свойств горных пород), эта феноменологическая теория отличается простотой и ясностью физических предпосылок, а также наглядностью графической интерпретации предельных состояний материалов, прочностные свойства которых она описывает. По этой причине именно эта терия положена в основу действующих норм проектирования.

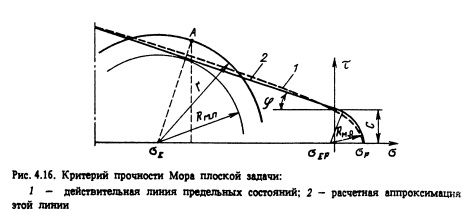
Важным вопросом при численной реализации критерия Мора является аппроксимация линии (рис. 4.16, поз. 1), ограничивающей область предельных состояний - огибающей предельных кругов Мора. Во многих работах данная линия аппроксимируется прямой, определяемой зависимостью вида

Аппроксимирующие параметры с и ср физически интерпретируются соответственно как сцепление и угол внутреннего трения грунта. Подобная аппроксимация обеспечивает удовлетворительную точность в диапазоне напряжений, соответствующих пологому участку линии предельных состояний. Более точной и вместе с тем удобной при численной реализации является кусочно-регулярная аппроксимация (рис. 4.16, поз. 2) линии предельных состояний критерия Мора. Участок вблизи предельной точки на оси о в этой аппроксимации описывается дугой окружности с центром в точке ОЕР и радиусом, вычисляемым по формуле

Входящий в условия (4.10), (4.11) коэффициент Киу характеризует степень близости Некоторой экстремальной точки (точка А, рис. 4.16) запредельного круга к линии предельных состояний. Условие (4.10) оценивает эту близость в направлении координатных линий; неравенство (4.11) соответствует минимальному значению поскольку исходит из оценки взаимного расположения запредельного круга г и линии предельных состояний критерия Мора.

При реализации итерационной схемы метода упругих решений или метода начальных напряжений указанные критерии используются для анализа допустимости вычисленных на очередной гй итерации напряжений. При этом в точках, где Км у < 1, осуществляется коррекция тензора напряжений в соответствии с принятым способом преобразования запредельных кругов Мора до допустимых размеров. Разность значений начальных и преобразованных напряжений определяет значение вектора невязки в решении, который используется для вычисления грузового вектора следующей итерации. В классической форме критерий Мора позволяет рассматривать только изотропные среды. Г.Н. Кузнецовым была предложена обобщенная форма критерия Мора (рис. 4.17), позволяющая рассматривать грунтовые массивы, ослабленные разноориентированными системами трещин и напластований. Как видно из рисунка, обобщенный критерий помимо прочности массива в направлениях, не совпадающих с трещинами, определяемых линией LM, характеризует также прочностные свойства поверхностей трещин, область допустимых значений напряжений на площадках которых ограничивается линиями. Таких линий обобщенный критерий в принципе может включать несколько.

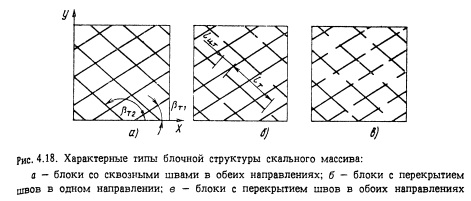
Модели, описанные выше, неявно предполагают непрерывность трещин. Такая предпосылка вполне корректна до тех пор, пока длина трещин превышает характерные размеры выработок. В противном случае прерывистую структуру трещин необходимо учитывать в расчетной модели. Нередко эту задачу решают путем вычисления приведенных прочностных характеристик квазинепрерывных трещин на основе способа континуализации (размывания) прочности целиков массива между ними. Такой подход вполне приемлем, если длина трещины существенно превышает размер целиков массива (рис. 4.18).

Другой подход к решению данной задачи основан на анализе кинематической возможности реализации предельного относительно плоскости трещин напряженного состояния. В отличие от способа размывания прочностных свойств он является корректным в случаях, когда размеры трещин и целиков массива соизмеримы. Для иллюстрации этого подхода рассмотрим массив, ослабленный двумя системами трансверсальных трещин с углами наклона зависимости от геометрических параметров

трещин при этом возможны три характерные модели блочного массива (рис. 4.18). При анализе напряженного состояния массива в итерационном процессе решения на базе указанных моделей нелинейных задач используется предположение о невозможности кинематической реализации в рассматриваемой точке запредельного (относительно поверхности прерывистой трещины одной из блокообразующих систем) напряженного состояния грунтового массива, если оно является при этом допустимым относительно поверхности трещин другой блокообразующей системы.

Оценка устойчивости выработок и определение параметров их анкерной крепи. Оценка устойчивости выработок выполняется на базе расчетных схем предельного равновесия, составляемых для потенциально неустойчивых грунтовых блоков (вывалов в своде, стеновых призм обрушения грунта). Возможные наиболее неблагоприятные конфигурации таких блоков строятся с учетом структуры трещиноватости массива в пределах, найденных с помощью описанных выше физически нелинейных моделей механики сплошных сред зон развития неупругих деформаций (рис. 4.19).

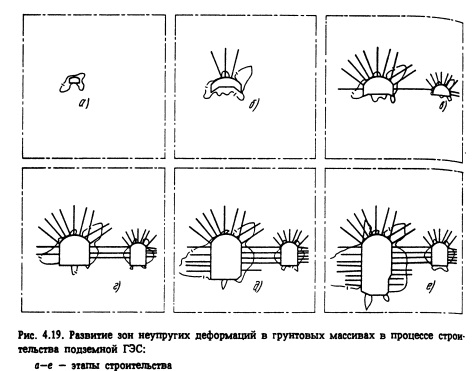
Вследствие блочной структуры скальных массивов, обуславливаемой ослаблением его разноориентированными системами трещин, поверхность, определяющая конфигурацию неустойчивых образований, имеет вид многогранника со ступенчатой в общем случае геометрией отдельных граней. При этом общая подвижка неус тойчивых блоков происходит в некотором направлении, задаваемом углом 0С по так называемым площадкам скольжения, совпадающим с одной из блокообразующих систем трещин, угол падения которой. В случае совершенной сети трещин, когда длина их существенно меньше размеров выработки (L), модуль трещиноватости, угол наклона отдельных граней 0К может приближенно оцениваться по формуле

В тех случаях, когда условие (4.16) не удовлетворяется, проектируется крепь выработок, рассчитанная на нагрузку в виде дефицита удерживающих сил.

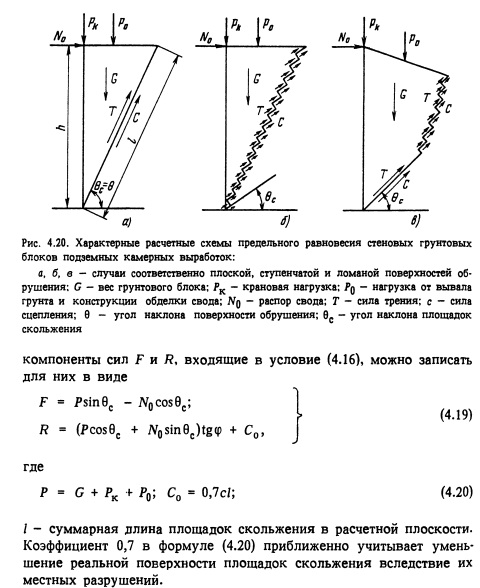
При рассмотрении наиболее широко распространенных в проектировании подземных ГЭС камерных выработок с корытообразной формой поперечного сечения оценка устойчивости в плоской постановке стеновых грунтовых блоков производится на базе расчетных схем, характерные типы которых изображены на рис. 4.20. Принимая в соответствии с [21] ус грунтовых блоков равным единице.

Длина анкеров определяется геометрией поверхности обрушения наиболее неблагоприятного в этом смысле неустойчивого стенового грунтового блока. Общие положения расчета сейсмонапряженного состояния сооружений. Сейсмическая нагрузка на подземные сооружения представляет собой деформационное воздействие, вызываемое прохождением в массиве продольных и поперечных волн, возникающих в очаге землетрясения, и характеризуется сейсмограммой (графиком изменения во времени смещений точек грунтового массива), велосиграммой (графиком изменения во времени скоростей смещения точек массива) акселерограммой (графиком изменения во времени ускорений смещения точек массива), а также направлением распространения сейсмических волн.

Реальное сейсмическое воздействие носит весьма сложный, хаотический характер, поэтому при моделировании оно, как правило, схематизируется в виде суммы периодических колебаний (гармоник). Согласно гл.7 СНиП-Н-7-81 сейсмическую нагрузку при проектировании подземных сооружений следует учитывать лишь для районов, подверженных землетрясениям силой 7, 8, 9 баллов.

В настоящее время существует два подхода к решению задачи о сейсмонапряженном состоянии подземных сооружений: расчеты в квазистатической постановке и методами волновой динамики.

В основе квазистатического подхода лежит допущение о возможности пренебрежения изменением напряженного состояния массива, вызываемого сейсмическим воздействием, в пределах некоторой расчетной области, включающей выработку. Такой подход в целом ряде случаев вполне правомерен, так как длина сейсмических волн обычно на порядок превышает характерные размеры подземного сооружения и при этом распределение напряжений вокруг него аналогично статическому.

Напряжения на границе расчетной области, вызванные сейсмической нагрузкой в виде продольной волны (волны сжатия - растяжения), определяются зависимостями, предложенными Ш.Г. Напетваридзе: по площадкам, перпендикулярным направлению волны, принимаемый по СНиПИ-7-81; Kh - коэффициент, зависящий от глубины заложения, при глубине заложения до 100 м линейно изменяется от 1 до 0,5, а на глубине более 100 м принимается постоянным, равным 0,5.

Направление распространения волн вследствие неопределенности положения очага землетрясения, отражения их от свободной поверхности, многократного преломления и отражения от границ раздела слоев в массиве может быть любым по отношению к сооружению. Учесть эти факторы позволяет предложенная в ГЗО) методика, основанная на оценке наиболее неблагоприятного напряженного состояния в каждом сечении конструкции при различных сочетаниях совокупного действия волн разного характера любого направления в плоскости поперечного сечения сооружения.

Таким образом, в квазистатической постановке задача определения сейсмонапряженного состояния подземного сооружения сводится к расчету невесомой области с выработкой на заданные на ее границах статические нагрузки, определяемые зависимостями (4.21) - (4.23).

В отдельном случае особого сочетания нагрузок напряжения в элементах конструкций, вызываемые инерционными сейсмическими нагрузками от собственного веса, определяются по формуле

Изложенный выше подход к решению задачи о сейсмонапряженном состоянии правомерен лишь при рассмотрении подземных выработок, расположенных на большой глубине от относительно ровной горизонтальной поверхности земли.

В случае выработок глубокого заложения с выраженным гористым рельефом дневной поверхности решение осложняется в связи с тем, что помимо прямого воздействия сейсмической волны, распространяющейся от очага землетрясения, на сооружение начинает действовать система волн, отраженных от свободной поверхности содействие каждой из отраженных волн может быть смоделировано при этом на основе описанного выше подхода.

Если же подземное сооружение находится вблизи дневной поверхности, имеющей к тому же резко выраженный гористый профиль, то исходная посылка о стационарности сейсмонапряжений на границах расчетной области оказывается неприемлемой. В этом случае задачу о сейсмонапряженном состоянии подземного сооружения приходится решать в динамической постановке, рассматривая волновые уравнения механики деформируемых сред. Решение ищется с помощью одного из известных численных методов. Необходимо отметить, что реализация данной постановки численными методами имеет ряд специфических особенностей и отличается от задач статики значительно большей трудоемкостью вычислений, обусловленной введением дополнительной переменной - времени.

При решении задачи в волновой постановке сейсмическое воздействие задается непосредственно в виде сейсмограмм, велосиграмм и акселерограмм. Основным источником информации о характере и структуре сейсмических воздействий являются инструментальные записи землетрясений, которые осуществляют либо на поверхности земли, либо на малой глубине. Известно, что интенсивность сейсмических воздействий убывает с глубиной. Однако в настоящее время отсутствует достаточный объем данных натурных наблюдений, позволяющий установить закономерности затухания сейсмических колебаний. Поэтому при использовании в расчетах сейсмограммы или акселерограммы вопрос о трансформации сейсмического воздействия на глубину расположения выработки решается в каждом конкретном случае с учетом местных условий.

При решении тем или иным из описанных выше способов задачи о сейсмонапряженном состоянии сооружения в расчетах, строго говоря, следует использовать динамические характеристики грунтового массива и материалов конструкций, поскольку поведение их при сейсмических нагрузках в общем случае может существенно отличаться от статического. Оценка таких характеристик для реального массива на сегодня представляет значительные сложности.

Полученное в результате решения рассматриваемой задачи поле напряжений складывается со статическим полем, после чего выполняется анализ несущей способности сооружения для соответствующего предельного состояния.

Пример решения характерной задачи. Как уже отмечалось выше, Наиболее распространенной для крупных камерных выработок типа машинных залов ГЭС является корытообразная форма поперечного сечения. Для крепления кровли таких выработок традиционно применялись конструкции обделок в виде железобетонных ци линдрических сводов. Однако в условиях превалирования горизонтальных тектонических напряжений подобные жесткие конструкции сводов практически не в состоянии обеспечить необходимой несущей способности из-за перенапряжения, возникающего вследствие деформаций разуплотнения массива при раскрытии нижних ярусов сечения выработок [61. В связи с этим возникла проблема найти такое решение свода, которое, сохраняя устойчивость контура выработки, вместе с тем было бы достаточно податливым, чтобы позволить конструкции уходить от восприятия чрезмерных деформаций.

С подобной проблемой пришлось столкнуться при проектировании крепей сводов камерных выработок Рогунской ГЭС. Для ее решения в НИС Гидропроекта было проведено комплексное расчетноэкспериментальное исследование. Расчеты выполнялись на базе описанных выше плоских физически нелинейных моделей МКЭ, эксперименты - на моделях из эквивалентных материалов.

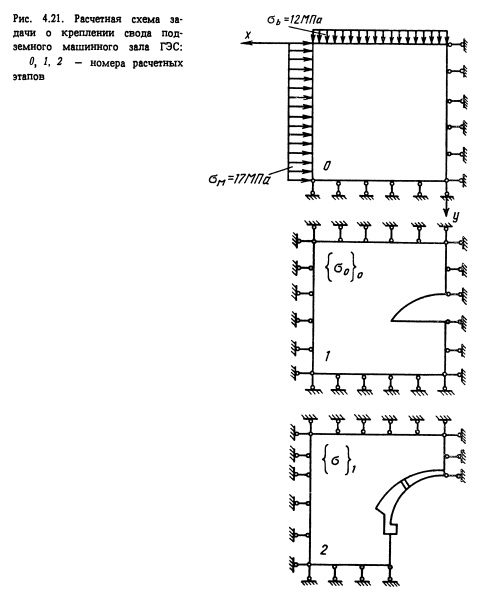
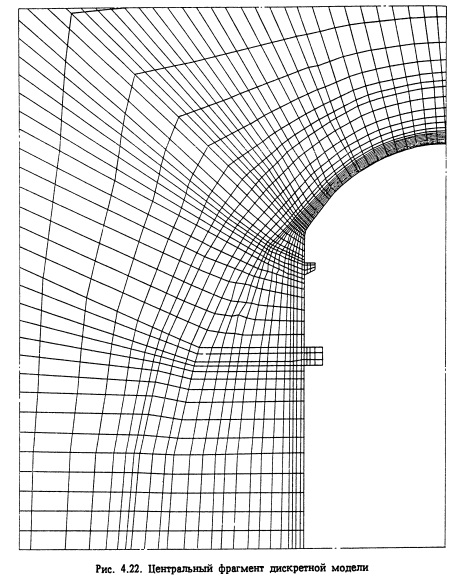
Исследование на математических моделях включало рассмотрение ряда различных вариантов конструктивного решения крепления сводовых частей выработок Гб]. Для сравнения рассматривался также вариант обычной жесткой” конструкции свода. Расчеты проводились на базе СНРС (рис. 4.21), включающей три этапа (аналогичная схема была принята и при физическом моделировании). С целью упрощения задачи в указанной СНРС были реализованы следующие допущения: во-первых, выработка рассматривалась как одиночная (т.е. влиянием смежных выработок пренебрегалось) с сечением, симметричным относительно вертикальной оси; во-вторых, не учитывался градиент естественных напряжений, обусловленный гравитационными силами (т.е. рассматривалась невесомая область), в-третьих, было решено пренебречь влиянием различия конфигураций сводовой и нижней частей выработки на НДС сооружения. Указанные упрощения позволили свести задачу к рассмотрению четвертой части полной расчетной области и благодаря этому более детально отразить в расчетной схеме особенности различных вариантов конструкции свода. Дискретная модель начального этапа СНРС включала 2376 КЭ. Конструкция свода моделировалась в ней шестью слоями четырехугольных КЭ. Центральный фрагмент дискретной модели последнего этапа СНРС изображен на рис. 4.22.

Массив в исследованиях рассматривался как однородный и изотропный со следующими приведенными характеристиками: модуль деформаций Е; коэффициент Пуассона v = 0,3;

На рис. 4.23 приведены результаты расчета для четырех из рассмотренных вариантов: первый вариант (рис. 4.23, а) - обычная жесткая конструкция железобетонного свода; второй (рис. 4.23, б) - цилиндрическая оболочка свода, имеющая два продольных деформационных шва; третий (рис. 4.23, в) - по контакту кровли со сводом предусмотрена податливая на сдвиг прослойка; четвертый (рис. 4.23, г), реализованный в проекте вариант, - комбинация второго и третьего - наряду с продольными деформационными швами в нем над средней секцией свода предусмотрена податливая антиадгезион- ная прослойка. Из рассмотрения приведенных на рисунке результатов можно сделать следующие основные выводы:

1) жесткая конструкция свода не в состоянии воспринять деформации кровли выработки, возникающие при разработке ее сечения: наблюдается ее разрушение в зонах пят и шелыги свода;

2) наличие податливой прослойки по всей поверхности контакта свода с массивом без устройства продольных деформационных швов лишь изменяет характер напряженного состояния конструкции, не обеспечивая ее несущую способность;

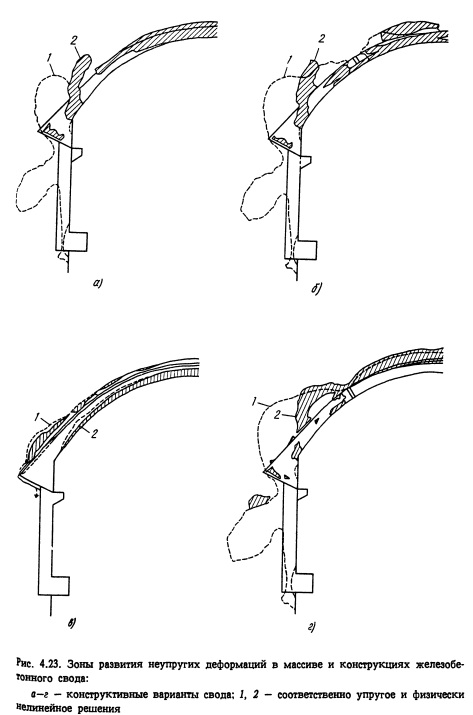
3) устройство в конструкции железобетонного свода только продольных деформационных швов приводит лишь к местному эффекту, не меняя характера его работы в целом;

4) комбинированный вариант обеспечивает работоспособность конструкции свода за счет рационального использования несущей способности грунтового массива.

Из сравнения приведенных результатов для упругой и физически нелинейной моделей следует также важный вывод о недопустимости применения первой для решения подобных задач вследствие существенного (не только количественного, но и качественного) искажения действительной картины НДС сооружения.

Данные физического эксперимента качественно подтвердили основные результаты и выводы теоретического исследования.

Подземные сооружения гидроэлектростанций. - М.: Энергоатомиздат, 1996.