Принципы статических расчетов обделок

Общие расчетные положения. Основополагающие принципы решения задач расчета туннельных выработок определяются фундаментальными требованиями метода предельного равновесия, лежащего в основе современных норм проектирования. Последний предусматривает необходимость рассмотрения при проектировании сооружения двух групп его предельных состояний:

по потере несущей способности или полной непригодности к эксплуатации;

по непригодности к нормальной эксплуатации.

Согласно [26] к первой группе предельных состояний рассматриваемых сооружений относятся состояния, характеризуемые потерей общей устойчивости выработки как вследствие нарушений прочности грунтового массива в приконтурных зонах, так и в результате потери несущей способности конструкций обделки. Ко второй группе относятся состояния, при которых наблюдается раскрытие трещин в бетонных (железобетонных) конструкциях обделки, ( снижающие ее долговечность, а также характеризуемые сверхнормативным значением фильтрационного расхода воды из туннеля.

Исходными данными для расчетов являются нормативные значения характеристик свойств материалов сооружения и нагрузок. Предельные состояния первой группы рассматриваются с применением расчетных (ухудшенных по сравнению с нормативными) значений нагрузок и характеристик свойств материалов обделок и грунтов. Состояния второй группы рассматриваются с применением их нормативных значений.

Нагрузки и воздействия разделяются на постоянные и временные - длительные, кратковременные и особые. К группе постоянных нагрузок на рассматриваемые сооружения относятся: собственный вес конструкций, воздействие их предварительного напряжения и горное давление. Последний вид воздействий является весьма специфическим: в конечном счете характер и интенсивность его проявления определяются свойствами обделки (крепи) и в значительной мере грунтового массива, в частности такой важной его характеристикой, как естественное напряженное состояние. Существуют две основные разновидности проявления горного давления: в виде неустойчивых грунтовых образований в приконтурной зоне выработок (вывалов, стеновых призм обрушения), так называемая консервативная нагрузка, и усилий контактного взаимодействия обделки с массивом, меняющихся в процессе их совместного деформирования при раскрытии (разработке) сечения выработок - неконсервативная нагрузка. Для обделок туннелей, устанавливаемых в непосредственной близости к забою, определяющей является вторая форма проявления горного давления, а для устанавливаемых со значительным отставанием от забоя более характерна первая.

К временным длительным нагрузкам относятся внутреннее давление воды (внутренний напор) в туннеле и воздействия, обусловленные наличием подземных вод. Последние имеют двоякую природу: гидродинамическое давление в виде объемных сил в массиве, возникающих при наличии фильтрационного процесса, и гидростатическое (остаточное при наличии дренажа) внешнее давление воды на обделку.

Учет указанных временных нагрузок в одном сочетании является благоприятным для обделок туннелей. Однако поскольку давление подземных вод в большинстве случаев подвержено влиянию многих факторов (сезонные колебания кривой депрессии, изменения фильтрационных свойств грунтов на трассе туннеля и др.) и вследствие этого может в большом диапазоне менять свое значение, такое сочетание допускается как исключение при наличии гарантий стабильности равномерного минимального наружного давления во всех (включая аварийные) эксплуатационных ситуациях. При этом в расчетах по первому предельному состоянию коэффициент надежности по нагрузкам для давления подземных вод принимается равным единице, т.е. в расчетное сочетание вводится его нормативное значение.

Из особых воздействий наиболее характерным является сейсмика. Сейсмическая нагрузка учитывается в расчетах обделок туннелей, сооружаемых в районах с сейсмичностью 7-9 баллов по шкале Рихтера. В большинстве случаеи, особенно для выработок глубокого заложения, удовлетворительные результаты обеспечивает квазистатическая постановка задачи. Для решения данной задачи в указанной постановке обычно используется изложенная в [30] методика, согласно которой для некоторого известного диапазона значений углов, характеризующих направление подхода сейсмических волн к сооружению, находится наихудшая из возможных комбинаций фаз сжатия, растяжения и сдвига продольных и поперечных их составляющих.

Типы расчетных схем. Расчетные схемы, используемые в настоящее время для решения описанных выше задач, условно разделяются на два принципиально различных типа. В схемах первого тина объектом исследования является конструкция обделки, которая представляется в виде цилиндрической или призма- тической оболочки или ее стержневой аппрокси- мации. Связь обделки с массивом и его деформационные свойства моделируются в таких схемах путем задания упруго распределенного основания либо сосредоточенных опор винклеровского типа.

Характерная особенность расчетных схем данного типа заключается Е том, что активное воздействие массива на обделку (горное давление) задается как известная консервативная нагрузка. Последнее обстоятельство в основном и определяет область их использования: расчеты на внутреннее и внешнее гидростатическое воздействие, воздействие начального напряжения конструкции, температурные задачи и т.д.

При рассмотрении основного вида воздействия - горного давления такие схемы могут использоваться с достаточной степенью приближения лишь для условий так называемого сводообразования [1], когда в массиве вокруг выработок образуется некоторая устойчивая форма в виде несущего породного свода. Назначение обделки в этом случае - воспринимать нагрузку от неустойчивого грунтового образования, конфигурация которого определяется геометрией выработок и расчетным очертанием указанной устойчивой формы. При этом достоверность решения полностью определяется точностью оценки такой нагрузки. Определить ее в общем случае весьма затруднительно, так как она является результатом сложного взаимодействия массива с обделкой и, следовательно, строго может быть оценена только на основе решения соответствующей контактной задачи. Тем не менее, такие схемы широко используются в проектной практике.

Подобные схемы применительно к задачам механики подземных сооружений рассматривались еще в конце прошлого века. Среди методов, ориентированных на достаточно эффективные вычислительные средства, и прежде всего ЭВМ, необходимо отметить известное решение, реализующее аппарат механики стержневых систем, предложенное Б.П. Бодровым и Б.Ф. Матэри для обделки кругового очертания, в последующем получившее название метода Метрогип- ротранса. В исходном виде расчетная схема этого метода включала в качестве известных границы зон активного и реактивного воздействия массива на обделку. Считается, что в пределах активной зоны действует заданная консервативная нагрузка. Нередко для определения этой зоны используют также термин зона отлипаний подразумевая участок отрыва обделки от массива. Название реактивная зона” определяет участок непрерывного контакта обделки с массивом, где она воспринимает его реактивный отпор при деформациях.

Изложенное решение явилось крупным шагом в развитии расчетных методов исследования конструкций подземных сооружении Однако даже применительно к условию сводообразования оно оставалось в значительной степени приближенным, так как в качестве известного требовало задания искомой величины - размера активной зоны, являющейся функцией деформированного состояния обделки.

С началом широкого внедрения в расчетную практику ЭВМ методика Метрогипротранса стала быстро развиваться. Одним из принципиальных ее изменений явился отказ от априорного задания активной и реактивной зон. Это оказалось возможным благодаря уточнению условий контакта на основе введения в рассмотрение упругих стержней (не воспринимающих растягивающих усилий), моделирующих отпорные свойства массива. Данное уточнение существенно изменило характер расчетной схемы, переведя ее в класс структурно-нелинейных в связи с возникновением так называемой проблемы односторонних связей [23].

В последнее время разработаны качественно новые продолжения описанной методики в направлении дальнейшего уточнения условий контакта обделки с массивом. В частности, имеется возможность задания начальных усилий в упругих связях, моделирующих отпорные свойства грунтового массива, что существенно расширяет возможности расчетных схем рассматриваемого типа, поскольку нагрузка на обделку в виде горного давления носит уже не консервативный характер, а изменяется в процессе деформации.

Следующим важным шагом в развитии рассматриваемых расчетных схем стал учет сил сцепления между обделкой и грунтом. При этом упругие связи, моделирующие массив, дополнительно характеризуются параметрами, определяющими их несущую способность на восприятие деформации отрыва. Особый интерес учет данного фактора представляет при рассмотрении крепей в виде набрызг- бетонных покрытий поверхностей выработок.

Существенно более сложные случаи представляют собой различные пространственные задачи. Естественным обобщением рассмотренных плоских стержневых расчетных схем является представление обделок в этих случаях в виде пространственной стержневой системы. Однако использование их для расчета, например, таких сложных подземных сооружений, как узлы пересечения и развилки туннелей, весьма затруднительно и во многих случаях нецелесообразно. Последнее определяется неадекватностью трудоемкости задачи грубой приближенности получаемых результатов, обуславливаемой низкой достоверностью исходных данных: параметров грунтового массива, нагрузки от горного давления, сейсмических нагрузок, а подчас и геометрии самой конструкции обделки.

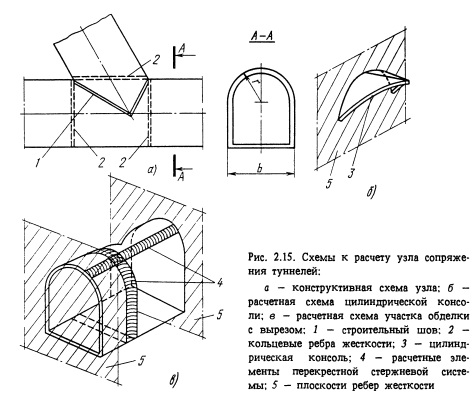
В ряде случаев такие задачи удается существенно облегчить за счет специальных конструктивных мероприятий, предусматриваемых как с целью упрощения технологии строительных работ, так и для создания условий работы конструкций обделки, соответству» ющих используемым для ее обоснования приближенным расчетным схемам. Например, одно из таких решений было реализовано в проекте узлов сопряжения строительных и отводящих туннелей Рогунской ГЭС. Конструкция одного из таких узлов изображена на рис. 2.15. По линии пересечения туннелей проходит деформационный шов, а для эквивалентного увеличения жесткости узла предусмотрены специальные диафрагменные элементы. Расчетная схема такого сопряжения распадается на две независимые части. Одна представляет собой цилиндрическую консоль, защемленную в плоскости пересекающей ее диафрагмы (рис. 2.15, б), а другая - участок призматической оболочки с характерным вырезом, также защемленной по торцам (рис. 2.15, в).

При рассмотрении второй, более сложной расчетной схемы реализовывался упрощенный вариант известного метода перекрестных стержневых систем [23], допускающий использование описанных выше плоских стержневых моделей. Обделка при этом представлялась в виде системы перекрестных плоских рамных и балочных элементов (4, рис. 2.15). Расчеты сводились к рассмотрению конечного множества различных по геометрии плоских стержневых моделей для соответствующих сечений каждого из направлений. При этом взаимное влияние смежных элементов одного направления не учитывалось. Отпорное воздействие элементов ортогонального направления моделировалось дополнительными упругими стерженьками. Податливость таких упругих связей оценивалась в предварительных расчетах каждой из плоских моделей на единичные воздействия, приложенные в соответствующих точках.

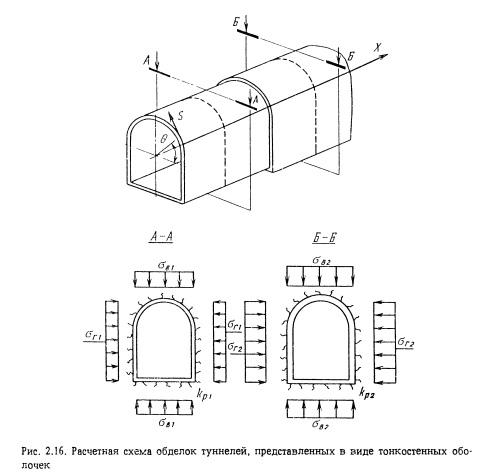
Более строгое в классе расчетных схем рассматриваемого типа решение пространственных задач позволяют получить оболочечные модели обделок туннелей. Напряженно-деформированное состояние обделки-оболочки описывается при этом известными дифференциальными уравнениями теории оболочек; массив горных пород, как и в приведенных выше схемах, моделируется основанием винклеровского типа (рис. 2.16).

Для оболочек вращения (в случае туннелей с круговой формой поперечного сечения) обычно используются разложения в ряды Фурье по угловой координате.

В случае оболочек с произвольной формой поперечного сечения приходится прибегать к универсальным, но вместе с тем и более сложным вариационным методам. Одно из наиболее эффективных решений обеспечивает метод Власова-Канторовича. Суть его заключается в том, что в качестве варьируемых (виртуальных) состояний в нем предлагается рассматривать характерные деформации поперечного сечения оболочки. При этом ее компоненты напряженного состояния поперечного направления определяются с помощью обычных методов расчета плоских рам.

К принципиально иному типу относятся расчетные схемы механики подземных сооружений, которые основаны на использовании моделей механики сплошных и дискретных сред. Их отличительная особенность заключается в том, что объектом исследования в них являются не только обделка, но и вмещающий выработку грунтовый массив. Для реализации таких расчетных схем широко используются методы теории упругости, пластичности и ползучести.

Внедрение таких схем началось с простейших осесимметричных задач. На основе этих схем анализируется напряженное состояние обделки, находящейся под действием внутреннего напора в упругой, бесконечной, однородной и изотропной среде. Решение такой задачи определяемся известными формулами Б.Г. Галеркина. Естественным развитием данной схемы явилась многослойная композиция круговых колец. Физическими предпосылками для ее введения явились комбинированный характер самой обделки и наличие вокруг нее кольцевых пластов с различными физико-механическими свойствами - зон заполнительной и укрепительной цементации, разуплотнения массива вокруг выработки и др. В математическом плане такая модель формулируется как многоконтактная задача Ляме для кругового кольца.

Существенным качественным развитием аналитических методов механики подземных сооружений явилось решение Н.Н. Фотиевой, позволяющее рассматривать туннели с произвольной формой поперечного сечения в задачах о внутреннем напоре и действии сейсмической нагрузки.

Расчетные схемы механики сплошных сред позволяют в принципе более точно и полно моделировать работу подземных сооружений, нежели рассмотренные выше схемы первого типа. Однако уже на ранней стадии внедрения таких схем стало очевидно, что их реализация обладает определенной спецификой, обусловленной естественным начальным напряженным состоянием массива. Некорректный учет этого фактора является причиной наблюдавшихся до сего времени серьезных методических ошибок [8].

Остановимся на двух характерных подходах к построению расчетных схем второго типа. Один из них примечателен тем, что заданное воздействие описывается в расчетной схеме, моделирующей готовое сооружение, аналогично схемам первого типа. Такой подход, повсеместно использовавшийся в строительной механике до начала семидесятых годов, получил название мгновенного загру- жения (М3). Использование схемы М3 в задачах механики подземных сооружений носит приближенный характер и в принципе весьма ограничено.

Другой подход к построению расчетных схем позволяет моделировать в них историю (генезис) формирования НДС сооружения, включая процесс его строительства. В результате решение задачи сводится к последовательному рассмотрению различных структурных состояний таких расчетных схем. отражающих предстроительные и характерные строительные этапы. Таким образом, НДС сооружения оказывается разрывной функцией, нелинейно зависящей от изменения их структурных параметров. В отличие от схем М3 подобные расчетные схемы уместно определить как структурно нелинейные (СНРС).

Принципиальным отличием СНРС подземных объектов от аналогичных схем наземных сооружений является необходимость описания в них этапа, моделирующего некоторый условный генезис поля естественных напряжений. Нарушение его равновесия на последующих строительных этапах вследствие раскрытия выработки, собственно, и определяет основной вид воздействия на сооружение.

В настоящее время при рассмотрении реальных объектов достаточно глубокого заложения поле естественных напряжений в массиве принимается однородным, характеризуемым параметром

определяющим отношение горизонтальных компонент нормальных напряжений к вертикальным, в связи с чем его уместно определить как коэффициент горизонтальных напряжений. В случае выработок неглубокого заложения, особенно с горным рельефом дневной поверхности, корректность задания и использования параметра X менее очевидна.

На формирование естественного напряженного состояния массива оказывают влияние два основных фактора: гравитационные и тектонические силы. В случае, когда тектонические силы выражены слабо, справедлива гипотеза Динника. При этом параметр X равняется коэффициенту бокового распора.

Моделирование генезиса естественных напряжений в массиве в общем случае осуществляется обычно путем задания объемных (гравитационных) сил и (или) распределенных на свободных (не закрепленных) границах расчетной области соответствующих компонент естественных напряжений.

Ошибки, о которых говорилось выше, как раз и связаны с процедурой моделирования генезиса естественных напряжений в массиве, что недопустимо совмещать со строительным и эксплуатационным этапами. Именно эта причина обуславливает недопустимость применения в общем случае для решения задач механики подземных сооружений схем М3, в которых такое совмещение имеет место, поскольку при этом НДС конструкций будет отличаться от действительного на величину, определяемую дополнительными фиктивными деформациями, не существующими в реальности в силу естественного развития событий. На это обстоятельство впервые обратил внимание И.В. Родин. В качестве правильного решения он предложил рассчитывать систему массив-обделка на действие приложенных по контуру выработки так называемых снимаемых напряжений, т.е. напряжений (с обратным знаком), существовавших в массиве до проходки выработки на площадках, касательных к линии ее контура. При этом практически неявно вводилась в рассмотрение двухэтапная СНРС: на начальном этапе некоторым образом находятся напряжения в массиве, на следующем - моделируется раскрытие сечения выработки с одновременной установкой обделки (что практически соответствует технологии ее возведения прямо у лба забоя). Перемещения, вычисляемые на первом этапе, игнорируются, напряжения двух этапов суммируются.

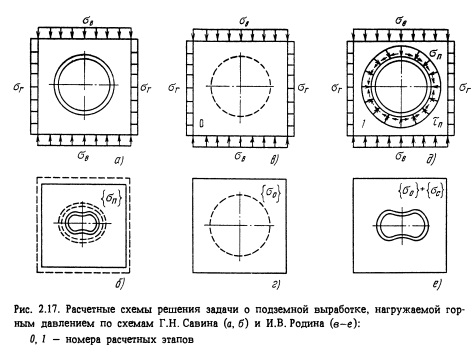
На рис. 2.17 показано различие в деформированном состоянии обделки при реализации схемы М3 в традиционном для нее вариан те граничных условий (рис. 2.17, а, б) и двухэтапной СНРС по И.В. Родину (рис. 2.17, в, д). Из рисунка легко видеть природу ошибки обуславливаемой применением схем М3. В отличие от второго решения (рис. 2.17, е) в первом (рис. 2.17,6) обделка включается в работу на дополнительные несуществующие деформации контура выработки, преобразующие его в эллипс, в соответствии с заданным значением

Изображенный на рис. 2.17, в начальный этап СНРС соответствует тривиальному случаю генезиса - после однородно и, следовательно, значения компонент напряжений известны в каждой точке. Тем не менее необходимость в нем очевидна. Во-первых, задача моделирования генезиса поля естественных напряжений далеко не столь проста в общем случае, например, для выработок неглубокого заложения. Во-вторых, в методическом плане при Реализации численных схем данный этап создает известные удобства даже в тривиальном случае генезиса.

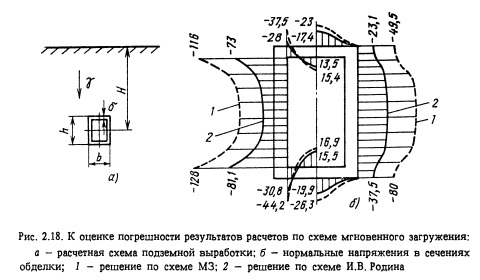
Количественное отличие в напряженном состоянии обделки туннеля при применении схем М3 и И.В. Родина можно проиллюстрировать примером решения модельной задачи, изображенной на Рис. 2.18. Из рисунка видно, что схема М3 приводит по сравнению со схемой И.В. Родина к завышению значений максимальных нагрузок в обделке более чем вдвое.

Моделирование на базе СНРС генезиса поля естественных напряжений не исключает ошибок той же природы, что и при использовании схем М3. Одна из наиболее характерных ошибок связана с рассмотрением массивов неоднородной микроструктуры, у которых поле естественных напряжений вследствие длительных релаксационных процессов стало квазиоднородным. Поскольку генезис, приведший к формированию такого поля, неизвестен, его нельзя смоделировать. Попытка з этом случае решить задачу стандартным образом, путем приложения заданных статических факторов к границам расчетной области (см. рис. 2.17, в), будет равносильна использованию схемы М3 применительно к некоторому природному объекту, который представляет собой участок рассматриваемой неоднородной области массива. В результате вместо однородного будет получено поле естественных напряжений с выраженными возмущениями, вызванными различием жесткостных свойств участков, составляющих макроструктуру грунтового массива. Аналогичная ошибка будет иметь место и при рассмотрении однородных, но анизотропных массивов.

Для того чтобы в приведенных выше и других случаях решить задачу моделирования генезиса естественного поля напряжений, характеризуемого параметром X, в расчетной схеме сооружения (СНРС) следует описывать необходимое количество предстроительных этапов, временно вводя в рассмотрение однородную изотропную область с некоторыми фиктивными деформационными характеристиками. Соответствующие задачи должны решаться в упругой постановке. В конце решения фиксируются только значения компонент напряжений в точках; перемещения игнорируются. На первом же строительном этапе в СНРС производится замена фиктивных характеристик свойств массива действительными.

Приемы моделирования на базе СНРС некоторых технологических и конструктивных факторов. Главная задача исследований туннелей заключается в поиске наиболее рационального решения конструкции обделки и обоснование ее надежности. Основным принципом решения таких задач является проведение целенаправленной серии численных экспериментов с указанными расчетными моделями. Количество и содержание таких экспериментов определяется способами, посредством которых инженеры-проектировщики добиваются наиболее благоприятного НДС обделки в наихудшей комбинации воздействия на нее.

Одним из наиболее эффективных способов является регулирование значения горного давления, действующего на обделку. Решение задачи определения оптимального значения отставания возведения обделки от забоя в любом случае может быть получено только на базе СНРС, моделирующих призабойный участок туннеля.

Достаточно приемлемое решение может быть получено и на базе плоской СНРС. Для этого после этапа, моделирующего генезис поля начальных напряжений, описываются этапы, по существу моделирующие известную в горном деле и иногда используемую в подземном строительстве операцию перекрепления. Идея решения заключается в следующем.

Как известно, деформации контура выработки затухают по мере продвижения забоя (рис. 2.19, а). При этом упругие деформации (заштрихованная область) при раскрытии очередной заходки реализуются практически мгновенно и затухают (иу) на расстоянии около 15-2 характерных размеров сечения выработки. Неупругие деформации, связанные с процессом разуплотнения массива и его локальными подвижками по различным системам трещин, затухают гораздо медленнее и поэтому расстояние dn до места их стабилизации (ип) от лба забоя существенно увеличивается. Чем дольше время тухания, тем больше dn. При длительных остановках забоя с течением времени, начиная от f0, неупругие деформации нарастают и в который момент времени стабилизируются, причем зона бухания ординат их эпюры dnk приближается к упругой. Зависимости u(t) могут быть получены на базе натурных наблюдений в начале каждого характерного в инженерно-геологическом отношении участка трассы.

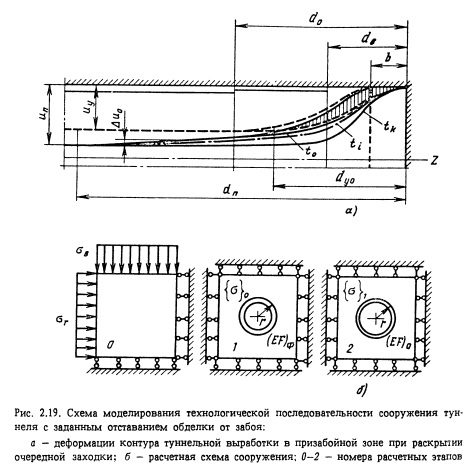
На следующем этапе выполняется операция перекрепления: удаляется фиктивная обделка и вставляется заданная, которая воспринимает на себя нагрузку, соответствующую оставшейся части деформаций контура.

Погонную фиктивную жесткость (EF) можно приближенно определить рассматривая приведенную круговую обделку радиусом, нагруженную по контакту с массивом гидростатическим горным давлением q. Кольцевые усилия N в ней будут определяться при этом формулой

Рассматривая фиктивную обделку как бесконечную тонкую цилиндрическую оболочку, находящуюся в условиях осесимметричной деформации, можно записать, что в пределе дает известное выражение упругих смещений круговой выработки. Таким образом, значение, определенное по Формуле (2.28), дает лишь нижнюю границу, соответствующую доле полных упругих смещений. Для учета неупругой составляющей Смещений (EF) следует пропорционально увеличить.

Предположим теперь, что на некотором расстоянии db от забоя перед постоянной обделкой устанавливается временная крепь (анкеры, арки, набрызг-бетон, черновой бетон и т.п.), назначение которой - обеспечить устойчивость свободной поверхности выработок до установки постоянной обделки, сохранив при этом запас несущей способности для совместного деформирования до величины ип в системе массив-временная крепь-постоянная обделка. В этом случае на первом строительном этапе СНРС вместе с фиктивной обделкой моделируется установка временной крепи заданной жесткости. При этом величина уменьшается на долю деформации, допустимой для данной крепи. Если временная крепь представляет собой систему достаточно часто расположенных анкеров, то в расчетной схеме можно учесть также повышение вследствие этого прочностных свойств массива на глубине их рабочей зоны (см. ниже). На следующем этапе временная обделка, естественно, сохраняется.

Описанная выше достаточно просто обобщается в случае, когда крепь выработки постепенно наращивается по мере увеличения деформации массива, путем установки новых элементов, включая конструкцию, завершающую на заключительном этапе формирование постоянной обделки. В этом случае количество промежуточных этапов в СНРС соответственно увеличивается.

Для достаточно устойчивых крепких скальных пород эффективным видом постоянной крепи является система анкеров с набрызг- бетонным покрытием. Параметры такой обделки определяются по методике, изложенной в [16]. При этом рассматривается СНРС, включающая неподкрепленную выработку. В результате из расчетов определяется конфигурация зон неупругих деформаций вокруг выработки. При умеренном размере такой зоны проектируется анкерная крепь с замками анкеров, выведенными за ее пределы. В качестве расчетной нагрузки на такую крепь рассматривается вес грунта в объеме потенциального вывала, расположенного в пределах неупругой зоны. Конфигурация вывала определяется с уче том структуры трещиноватости массива.

Характерной особенностью задач расчета туннельных выработок является необходимость моделирования контакта между обделкой и породой, особенно в кровле выработок, где в определенных условиях может наблюдаться отлипание обделки от породы. При опк сании условий контакта обычно используется прочностная моде основанная на критерии Кулона-Мора. Если рассматривается 0 делка, прианкеренная к породе, то параметры сопротивления отрыву орт и сдвигу ст этого критерия увеличиваются на основе к тинуализации (размазывания) сопротивления анкеров растяжению. Приведенные значения вычисляются при этом по формулам

Для безнапорных деривационных туннелей, проходимых в обводненных массивах с высоким уровнем грунтовых вод, нередко приходится прибегать к устройству дренажной системы, обеспечивающей снижение гидростатического давления на обделку до допустимого значения. В этих случаях возникает необходимость комплексного решения задачи. Сначала на базе общей СНРС решается задача стационарной напорной фильтрации, в которой дополнительно моделируется последовательность установки элементов дренажной системы. Найденные в результате решения этой задачи значения напорного поля и фильтрационные градиенты соответствующих этапов СНРС учитываются в виде дополнительных факторов в статической задаче: давление фильтрационного потока и остаточное гидростатическое давление на обделку.

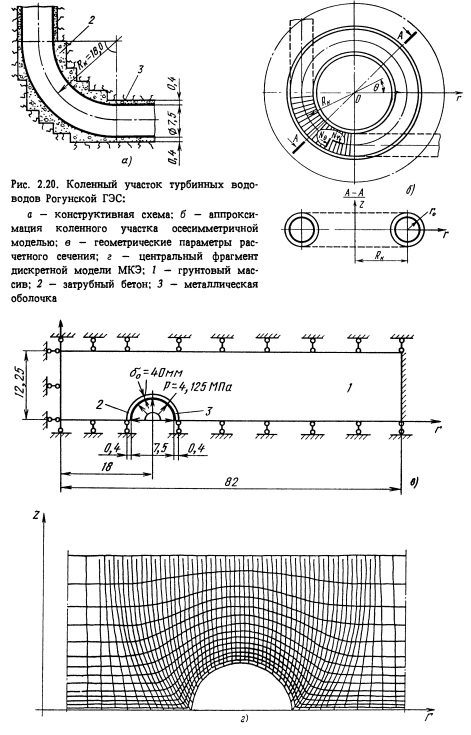
Пример решения одной из характерных задач. Компоновка высоконапорных водоводов энергетических трактов ГЭС и ГАЭС обуславливает наличие на их трассах криволинейных, так называемых коленных участков. По ряду причин (прочности, технологичности и т.п.) обделка коленных участков, как правило, включает металлическую оболочку. Нормы [24, 26] на этих участках, так же как и на регулярных, требуют при назначении толщины металлической оболочки учитывать отпор грунта. Для случаев разрешается пользоваться формулами плоской задачи [24], принимая при этом значения нормальных напряжений в поперечных сечениях. Для случаев в нормах на сегодня четкие регламентации отсутствуют, оговаривается лишь необходимость проведения специальных исследований.

В результате в целях обеспечения гарантии надежности работы сооружения металлическая оболочка колен при проектируется обычно как свободная, при этом напряжения оф оцениваются по известной котельной формуле. Такой подход, естественно, приводит к существенным материальным затратам.

Тем не менее достаточно строго учесть отпор грунта в этих сложных случаях позволяют осесимметричные расчетные схемы механики сплошных сред. Возможность их применения обосновывается слабым влиянием на напряженное состояние определяющей центральной части колена (сечение по биссектрисе угла закругления) примыкающих к нему линейных участков.

С помощью указанных расчетных схем подобная задача решалась при проектировании коленных участков турбинных водоводов Рогунской ГЭС, один из которых изображен на рис. 2.20. Поскольку сооружение металлической оболочки и затрубное бетонирование выполняются после проходки туннеля, начальным напряженным состоянием грунтового массива при определении НДС обделки от воздействия внутреннего напора можно пренебречь, что допускает возможность использования обычной схемы мгновенного загружения.

Исследование проводилось методом конечных элементов. Массив в расчетах рассматривался как квазиоднородный и изотропный. Характеристики элементов расчетной схемы приведены в табл. 2.4.

Размеры расчетной области (рис. 2.20, в) в направлении оси Z приняты равными половине расстояния между осями параллельных выработок трассы напорных водоводов.

В целях упрощения металлическая оболочка моделировалась одним слоем осесимметричных конечных элементов, что позволяло в данном случае с достаточной точностью оценить осевые усили. Расчеты выполнялись как в упругой, так и физически нелинейной постановках. В последнем случае на базе теории Мора моделировался процесс трещинообразования в затрубном бетоне и приконтурной зоне массива.

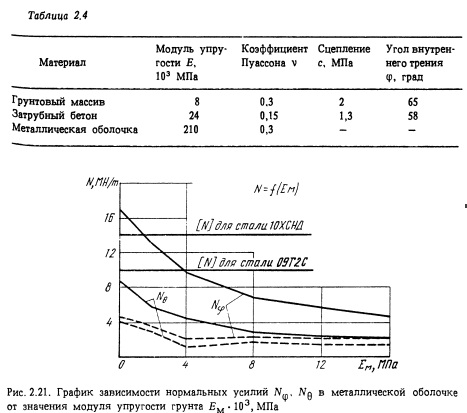
На основе серии численных экспериментов был построен график (рис. 2.21) зависимости усилий в металлической оболочке от значения модуля упругости грунта Е. Анализ этой зависимости позволил сделать вывод о том, что в рамках реального диапазона изменений деформационных свойств грунтового массива в приконтурной зоне выработки проектные параметры металлической оболочки обеспечивают избыточный запас ее несущей способности на восприятие расчетного значения внутреннего напора воды. Из рисунка видно, что по сравнению, например, со случаем свободной оболочки (Е = 0) для взаимодействующей с массивом уже при 6000 МПа толщину стали можно уменьшить вдвое. Анализ результатов расчетов также показал, что в рассматриваемом случае усилия продольного направления N0 составляют до 50% и более усилий поперечного направления.

Подземные сооружения гидроэлектростанций. - М.: Энергоатомиздат, 1996.