Методика расчетов надежности отдельных узлов тепловой схемы ТЭЦ
В качестве денежного критерия для технико-экономических расчетов могут быть использованы приведенные затраты. Структура приведенных затрат в энергетике описывается в общем виде выражением [2043. Запишем его в детерминированном виде
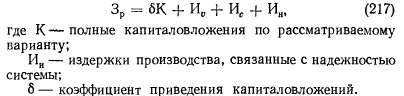
Наибольшее влияние на жизнеспособность схемы имеют котлоагрегаты, поэтому рассмотрим вначале методику расчета их надежности.
Представим выражение (217) в виде, позволяющем проанализировать его по условиям надежности котлоагрегатов:

В выражениях (219)—(221) можно пренебречь изменением топливной составляющей по вариантам, так как к. п. д. котлов производительностью 300—400 т/ч отличаются весьма незначительно и эта составляющая оказывается независимой от типоразмера котлоагрегата.
В соответствии с действующей методикой технико-экономических расчетов в энергетике рассматриваемые варианты сравнивают по разности приведенных затрат. Составляя разность любых двух выражений из трех (219)—(221), нетрудно убедиться в том, что величины Коб, Ит, И3об, Иа + Роб и И0об не влияют на выбор варианта, так как при вычитании сокращаются. Разность неполных приведенных затрат Зр совершенно строго равна разности полных приведенных затрат, но введение такой условной величины позволяет упростить дальнейшие расчеты.
Итак, неполные приведенные затраты по любому варианту
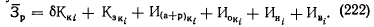
Определение первых четырех слагаемых выражения (222) является обычным для энерго-экономических расчетов и не представляет труда. Величина Зр представляет собой издержки производства, связанные с ненадежностью котлоагрегатов в течение расчетного периода, — одного года эксплуатации системы.
В течение рассматриваемого расчетного периода система или ее элементы (котлоагрегаты) могут находиться в следующих состояниях:
1) нормальное функционирование, работа;
2) ремонт плановый;
3) восстановление при случайном отказе;
4) включение, переключение;
5) отказ.
При этом имеется в виду, что период содержания в готовности к применению отсутствует, т. е. вероятность содержания в готовности равна единице. Каждое из вышеперечисленных состояний системы детерминировано или стохастически увязано с календарными периодами года, а следовательно, с уровнем тепловых и электрических нагрузок и ремонтов работы основного оборудования. Плановые ремонты— это состояние системы, которое можно наиболее строго детерминировать. При этом будем исходить из следующих положений.
1. Текущие ремонты котлоагрегатов проводятся два раза в год, капитальные — один раз в два года.
2. В периоды с температурами наружного воздуха ниже tc.x плановые ремонты не производят.
3. Промежутки времени между двумя смежными ремонтами для данного типа котлов принимают постоянными в течение всего ремонтного цикла.
В соответствии с этими положениями расчетный период оказывается разбитым на следующие этапы, отличающиеся возможным состоянием системы и уровнем тепловых нагрузок.
Этап I—I — расчетный режим, соответствующий наружным температурам ниже 4.0.
Этап II — II — расчетный режим, соответствующий наружным температурам ниже 4.x.
Этап III— часть III расчетного режима, характеризуемая отсутствием текущих и капитальных ремонтов.
Этап IV— часть III расчетного режима, характеризуемая наличием текущих или капитальных ремонтов.
Этап V — часть IV расчетного режима, характеризуемая отсутствием текущих и капитальных ремонтов.
Этап VI — часть IV режима, характеризуемая наличием текущих и капитальных ремонтов.
На каждом из этих этапов состояние системы может быть точно описано с энергетической, экономической и надежностной точек зрения. Тогда издержки производства, входящие в выражение (222) и связанные с надежностью, запишем в виде

Рассмотрим возможность распространения выражения (224) на любой элемент схемы. Очевидно, физическая сущность отказа системы определяется преимущественно снижением паропроизводительности котлоагрегатов. Отказ любого элемента этой системы непосредственно влияет на снижение мощности ТЭЦ и приводит к экономическим потерям от надежности. Отказ какого-либо элемента узла тепловой схемы ТЭЦ, назначение которого ¦— снабжать систему котлоагрегатов водой или топливом, влияет на снижение мощности ТЭЦ и экономический ущерб посредством влияния отказа этого элемента на отказ котла. Величина ущерба в этом случае будет определяться, кроме характеристики самого узла, еще и степенью влияния случайных отказов его элементов на вызываемые этими отказами остановки котла или котлов. Меру этого влияния оценим коэффициентом влияния Кв, который показывает, какая часть котельной мощности остается в работе при случайном отказе любого элемента рассматриваемого узла. Обозначим номинальную производительность элемента снабжающего узла, выраженную в тех же единицах, что и производительность котлоагрегата, через П. Тогда коэффициент влияния для снабжающего узла

При рассмотрении узлов, не снабжающих котлоагрегат водой или топливом (например, узел линейных связей в группе питательных насосов), необходимо вначале логическим анализом определить влияние элементов данного узла на элементы снабжающего узла, а затем рассчитывать по изложенной выше методике.
С помощью коэффициента влияния можно определить наличие резервных элементов в узле на рассматриваемом временном интервале. При Кв> 1 в схеме узла имеется резервный элемент в данном режиме, при Кв <С 1 резервный элемент отсутствует.
Отдельно стоящие бойлерные. Оптимальным режимом загрузки отопительного отбора турбин является использование номинальной величины его постоянно, в течение всего отопительного сезона, т. е. I, II и III расчетных режимов. Соответственно, и нагрузка бойлеров оказывается постоянной в этих режимах. Тогда для достаточных систем справедливо следующее равенство:

Полагая, что в любом из рассматриваемых избыточных вариантов количество резервных бойлеров целесообразно принимать большим единицы, записываем равенство (300) для избыточных схем в виде

Поскольку в заданной комбинации возможны разнотипные турбины, группы бойлеров могут отличаться как количеством элементов, так и ущербом, возникающим при отказе элементов каждой группы. Исходя из принципа несовместимости и независимости отказов, записываем
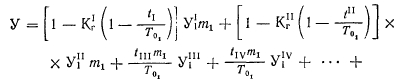

Для отдельных бойлерных время жизни элементов можно принимать равным длительности отопительного периода:

Выражения (313) и (314) описывают неполные приведенные затраты для группы бойлеров. Для заданной комбинации турбин, в которую могут быть включены разнотипные агрегаты, необходимо суммировать неполные расчетные затраты по каждой турбине или группе турбин в соответствии с зависимостью (305).
Встроенные бойлерные являются элементами оборудования турбин Т-110-130, Т-170-130, поэтому трудно наметить в этом случае поле поиска, т. е. конкурентные варианты выбора количества или структуры бойлеров. На дальнейших этапах исследования проблемы надежности может быть поставлена задача усовершенствования оборудования, при решении которой возможна оптимизация структуры встроенных бойлерных, дымососов, вентиляторов, горелочных устройств, привода питательных насосов и т. д. При этом может быть решена локальная задача — нахождение ожидаемых издержек производства для заданной структуры встроенных бойлерных при определенном варианте набора турбин.
У турбин с переключаемым отсеком с встроенными бойлерами конструктивно осуществляются две ступени подогрева сетевой воды, при этом первый, по ходу воды, бойлер является неотключаемым от турбины, а второй — отключаемым. Это накладывает отпечаток на оценку ущерба. При отказе первого бойлера необходима остановка турбины для восстановления отказавшего элемента, при отказе второго возможно его отключение на ремонт с соответствующим снижением выработки электроэнергии на тепловом потреблении.
Рассмотрим расчет надежности встроенных бойлерных, полагая вначале, что в заданном варианте турбин присутствуют только теплофикационные со встроенными бойлерами.
Количество последовательных элементов в I, II, и III режимах равно числу бойлеров:
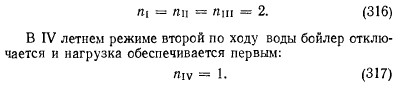
В связи с вышеизложенным среднее время жизни первого T0j и второго ТЬ, бойлера оказывается различным: для первого оно равно периоду между остановками турбины на ремонт, для второго — отопительному периоду. Следовательно,


В том случае, если в заданном варианте есть турбины со встроенными и групповыми бойлерами, то расчетные затраты должны определяться суммированием выражений (313) и (326).
Каждый из рассмотренных выше трех узлов: котлоагрегаты, питательные насосы, бойлерные — включают в себя трубопроводные связи и арматуру. Надежность этих узлов определяется надежностью структуры схемы и надежностью запорных и регулирующих органов.
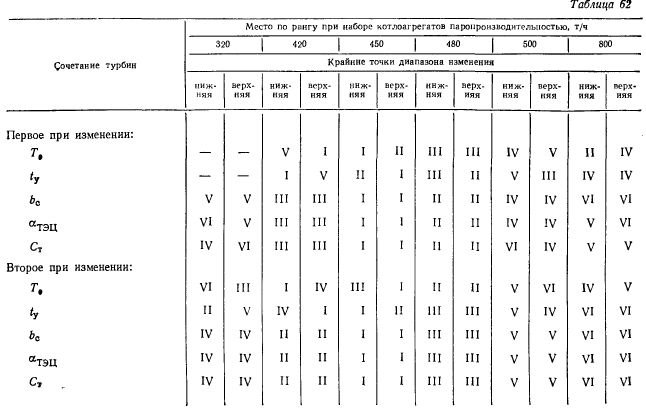
Для анализа полученного множества решений были применены три критерия теории игр: минимаксный (критерий Вальда), недостаточного основания (критерий Лапласа), минимального риска (критерий Сэвиджа). Для упрощения расчетов исследование велось по релаксационной схеме. Вначале для опорных значений ty проигрывались значения Т0 в упомянутом шаге, затем для базисного значения Т0 проигрывались соответствующие значения ty.
Так как на втором этапе расчета определялась область неоптимальных решений, анализу подвергались только оптимальные решения (структуры узла), находящиеся в конфликтной ситуации и смежные с ними.
Рассмотрим матрицы приведенных затрат для каждого сочетания турбин при случайных значениях Т0 = 1500, 2500, 3500, 4500, 5500, 6500, 7500 и 8500 ч.
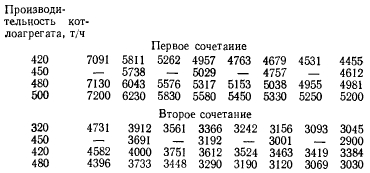
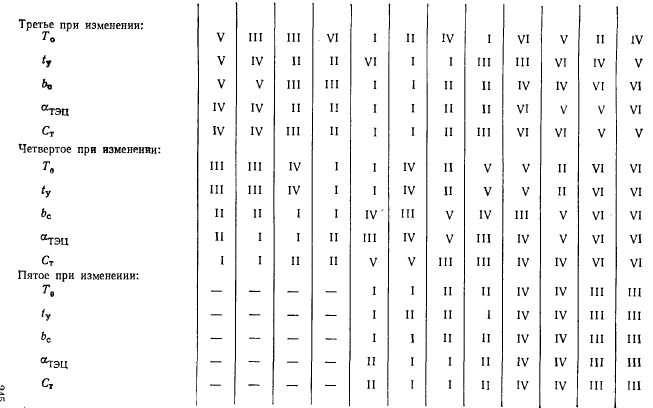


Для расчета критерия пессимизма-оптимизма рассмотрим вспомогательные матрицы значений риска при выборе различных вариантов котлоагрегатов. Рассмотрим указанные матрицы для каждого сочетания турбин при случайных значениях Т0 = 2500, 4500, 6500 и 8500 ч.

Рассмотрим эти же матрицы для каждого сочетания турбин при случайных значениях ty = 48 и 336 ч.


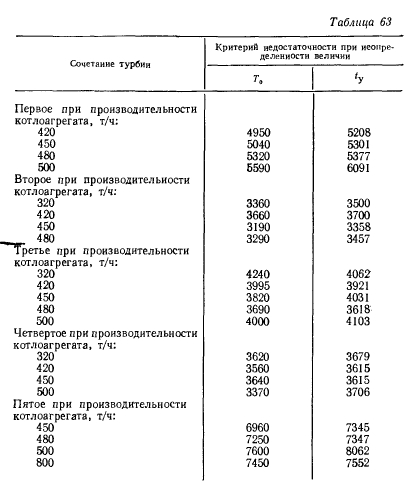
Значения критерия недостаточности основания при различных сочетаниях турбин приведены в табл. 63. Оптимальные типы котлоагрегатов по трем критериям для всех рассмотренных сочетаний турбин сопоставлены в табл. 64.
Для нахождения объективного оптимального решения необходимо сопоставить между собой решения, полученные по каждому критерию, с учетом их сильных и слабых сторон. Принято считать, что если альтернативная стратегия не связана с разумным противодействием или ее нельзя изменить за рассматриваемый в задаче отрезок времени, то рационально пользоваться критерием Лапласа, дающем в этом случае наиболее сильное решение.
Использованные критерии характеризуются следующими особенностями. Минимаксный критерий является частным случаем более общего критерия Гурвица. При этом показатель пессимизма — оптимизма принимается равным нулю, что свидетельствует о наиболее пессимистическом подходе. Применяя этот критерий, получаем наиболее осторожную оценку. Кроме того, характер функции цели определяет устойчивые минимумы в широком диапазоне изменений неопределенных величин, поэтому игровая ситуация существует соответственно в достаточно узком диапазоне неопределенности. Указанный критерий не является в этих условиях достаточно сильным.
Критерий пессимизма — оптимизма является достаточно сильным в связи со следующими обстоятельствами. Он основывается на принципе равновероятного распределения случайной величины, что соответствует вероятностной модели, заложенной в структуру функции цели. Использование этого критерия не зависит от соотношения минимумов и максимумов в матрице расчетных затрат и дает решение, одинаково сильное во всем диапазоне изменения случайных величин. Критерий Сэвиджа хорошо дополняет критерий Лапласа, так как позволяет выбрать решение, характеризуемое минимальным риском, что особенно важно при оптимизации на основе показателей надежности.
Таким образом, решения, совпадающие по критериям Лапласа и Сэвиджа, могут считаться объективно оптимальными.
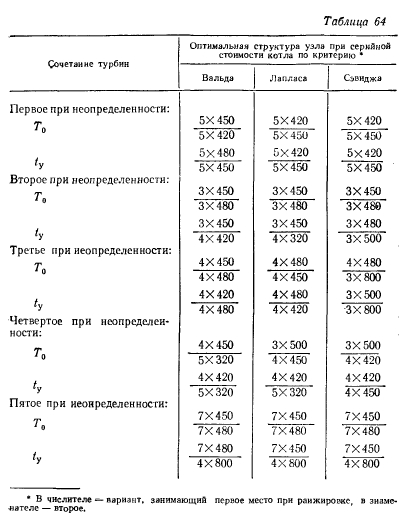
С учетом этого для первого сочетания турбин оптимальны наборы котлоагрегатов 5 х 420 т/ч, второго — 3 х X 450 т/ч, третьего — 4 х 480 т/ч, четвертого — 3 х X 500 т/ч, пятого — 7 х 450 т/ч.
Виноградов Ю. И., Векштейн Л. М., Соболь И. Д. ПРОМЫШЛЕННОЕ ТЕПЛОСНАБЖЕНИЕ. «Техника», 1975
