Определение количественных показателей надежности и эффективности

Надежность системы долго рассматривалась как качественная ее характеристика. По мере усложнения системы метод качественного анализа надежности все более и более входил в противоречие с растущими требованиями технологии их проектирования, изготовления и эксплуатации. Переход к количественному анализу надежности сложных систем требует учета большого количества разнообразных детерминированных и случайных факторов, всю совокупность которых можно оценить только с помощью аппарата теории вероятностей, теории случайных процессов и математической статистики.

Надежность изделия обусловливается прежде всего его безотказностью и работоспособностью. Отказом является событие, заключающееся в нарушении работоспособности. Безотказность и количество отказов на заданном интервале времени элементов системы или самих систем, спроектированных, изготовленных и эксплуатируемых идентично, имеют значительный разброс. Такое положение можно объяснить влиянием случайных факторовна работоспособность системы. Поэтому функциональное состояние системы в произвольный момент времени можно определять как случайное. Чтобы охарактеризовать случайную величину, достаточно указать, какие значения их вероятности она может принимать.

Указанный способ определения случайной величины приемлем, если она по условиям задачи может принимать конечное множество значений, однако количество таких задач весьма ограничено.

Значительно чаще приходится сталкиваться с задачами, при решении которых значения случайных величин несчетны. В этом случае прибегают к использованию понятия функции распределения случайной величины, т. е. вероятности того, что I принимает значение меньше, чем х для любых действительных значений аргумента [44]:

Распределение Пуассона. Случайная величина распределена по закону Пуассона, если она может принимать только неотрицательные целочисленные значения с вероятностями

Рассмотренные выше распределения случайных величин приведены для простейшего потока, отличающегося отсутствием стационарности, последствия и ординарности. Стационарность означает, что вероятность появления v событий в течение промежутка времени от Т до Т + t не зависит от Т, а зависит только от v и /. Отсутствие последствия означает, что вероятность наступления событий в течение промежутка ТХТ + т не зависит от того, сколько раз и как появлялись события v ранее. Ординарность означает невозможность появления двух или более событий за малый промежуток времени т:

Любое техническое устройство или схема состоят из элементов. Рассмотрим поведение элемента, представляя его жизнь из последовательных случайных переходов (из состояния функционирования в состояние отказа, далее в состояние восстановления и вновь в состояние функционирования). Такая картина наиболее близка к реализуемой в инженерных системах.

Предположим, что восстановление происходит мгновенно. Элемент начал свою работу в момент / = 0, и, проработав случайное время тх, выходит из строя. В этот момент он мгновенно заменяется новым, который, проработав время т2, также выходит из строя и заменяется элементом с временем работы т3. Процесс продолжается неограниченно. Закон распределения случайных величин

Опишем закон распределения, заданный выражением (156), для некоторых из перечисленных выше известных функций распределения.

Отсюда вытекает, что для большого участка времени среднее число отказов, приходящихся на единицу времени, близко к величине, обратной среднему времени жизни элемента.

Рассмотрим теперь модель процесса отказов и восстановлений элемента с конечным временем восстановления. Важной характеристикой надежности в этом случае является коэффициент готовности КР (t), равный вероятности того, что в момент t элемент находится в исправном состоянии

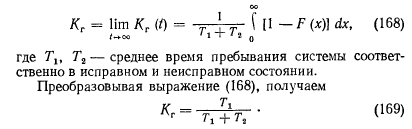
Для процесса восстановления с конечным временем характерны две случайные величины: vx () — число отказов на интервале (0, t) и v2 (t) — число восстановлений на том же интервале. Очевидно, эти две величины могут отличаться друг от друга самое большее на единицу. Рассмотрим моменты восстановлений. Расстояния между соседними моментами являются случайными величинами, распределенными по закону

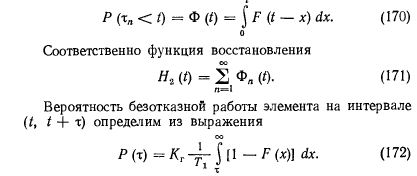
При экспоненциальном законе распределения длительность жизни и длительность восстановления функции распределения соответственно имеют вид

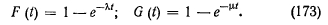
Вероятность нахождения элемента в состоянии работы — коэффициент готовности

Если время восстановления элемента конечно, но несоизмеримо с временем жизни элемента, то зависимости (168) — (175) теряют практический смысл, так как при Г2 Тх /Сг -> 1. В этом случае можно пользоваться зависимостями, предложенными для элементов с мгновенным временем восстановления. Коэффициент готовности — это средняя доля времени, которое система пребывает в исправном состоянии. Из этого определения вытекает, что вероятность безотказной работы элемента с конечным временем восстановления т равна произведению вероятности того, что в начальный момент времени застанем систему исправной, на вероятность исправной работы элемента в течение времени т для процесса с мгновенным восстановлением:

Понимая под системой совокупность технологически связанных между собой элементов с заданной степенью надежности каждого из них, будем говорить, что все элементы в системе соединены последовательно (в смысле надежности), если отказ хотя бы одного из них приводит к отказу системы. Элементы в системе соединены параллельно, если отказ только всех элементов приводит к отказу системы. Возможны схемы с комбинированным соединением элементов.

Рассмотрим систему из последовательных элементов с мгновенным восстановлением. Допустим, что элементы системы независимы, т. е. состояние одного не влияет на надежность другого. Очевидно, получаем поток отказов, в котором суммируется л процессов восстановления:

Рассмотрим характеристики системы с конечным временем восстановления. При этом будем предполагать, что во время восстановления одного элемента все другие продолжают работать. Каждый элемент оказывает и восстанавливается независимо от других. Коэффициент готовности такой системы равен произведению коэффициентов готовности ее элементов:

Время восстановления различных элементов тепловой схемы ТЭЦ 400—500 ч. Длительности I и II расчетных режимов соизмеримы с указанным временем восстановления, III и IV режимов — значительно превышают это время. Процесс в I и II режимах следует рассматривать как процесс с конечным временем восстановления, а в III и IV режимах — с мгновенным. Тогда функции восстановления элементов запишем следующим образом:

Так как функция восстановления численно равна среднему количеству отказов, происшедших до заданного момента времени, то выражение (200) количественно оценивает надежность рассматриваемого узла схемы.

В качестве общего критерия для любых систем может быть принята полезность их использования в стоимостном выражении, определенная на основе количественных характеристик надежности. В энергетических системах полезность наиболее адекватна производительности (выработка тепла и электроэнергии).

Связь между показателями надежности и эффективности может быть определена из выражения

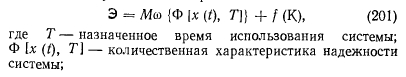
Очевидно, выражение (201) характеризует ожидаемые затраты на эксплуатацию системы за время Т и начальные капиталовложения, определяющие ее надежность. Из множества вариантов реализации системы предпочтение должно быть отдано той, у которой значение минимально. Выражение (201) является общим критерием полезности любой системы. Рассмотрим некоторые особенности этого выражения применительно к системам теплоснабжения, в качестве времени использования которой целесообразно принимать год ее жизни. За этот период система проходит некоторые состояния, отличающиеся координатами текущего времени, производительностью, режимом работы элементов, наличием или отсутствием плановых ремонтов, случайных отказов и восстановлений. Таким образом, фазовое пространство системы представляет собой совокупность точек, определяющих надежность системы в заданный момент времени. Так как полное состояние системы в произвольный момент времени зависит от многих переменных, то аналитически сложно описать траекторию движения системы в фазовом пространстве, учитывая, что на отдельных отрезках траектории параметры системы имеют детерминированное, стационарное значение. Поэтому целесообразно вычислять значение функционала на каждом из этих участков отдельно, суммируя затем полученные результаты: i=i

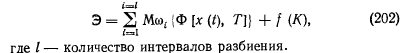
Выражение (202) тождественно выражению для приведенных затрат, которые используются в энерго-экономических расчетах. Приведенные затраты с учетом вероятностного характера дополнительных издержек, связанных с характеристикой надежности системы, запишем на основании формулы (202) в виде ш

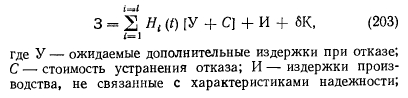
В состав издержек производства, не связанных с надежностью, входят затраты на топливо, зарплату, амортизацию, общие и прочие. Пользуясь выражением (203), будем решать локальные задачи для однородных систем, вариантных в смысле количества элементов и их структурных связей. Выбор турбин в тепловых схемах ТЭЦ оптимизируется вне категорий теории надежности и для расчета тепловой схемы по условиям надежности должен быть задан. Заданное сочетание турбин и определяет ту локальную задачу, в рамках которой варьируются остальные узлы тепловой схемы. Набор всех заданных комбинаций турбин является полем поиска, которые, в свою очередь, есть детерминированный параметр фазового пространства системы.

Эффективность всех остальных элементов системы, кроме турбин, не зависит от изменения тепловых нагрузок. Например, изменение производительности котлоагрегата или питательного насоса от 100 до 50% (от номинального значения) практически не влияет на относительный расход топлива в различных вариантах реализации тепловой схемы ТЭЦ.

Таким образом, отпадает необходимость введения еще одной группы переменных — тепловых нагрузок, которые могут приниматься постоянными для данной задачи (набор турбин), что определяет постоянство топливной составляющей и некоторых других затрат, связанных с машинным цехом. Издержки, связанные с вариантностью узла (например, заработная плата персонала котельной, амортизационные отчисления по котельной), являются переменными величинами в границах рассматриваемой задачи. На основании изложенного, уравнение (203) запишем в виде

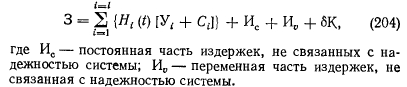
В соответствии с нормативными рекомендациями по технико-экономическому расчету выбор варианта осуществляется на основании разности приведенных затрат.

Для условий одной задачи при заданном наборе турбин и стационарных тепловых нагрузках постоянная часть издержек может быть исключена, а оптимизируемая величина записана в виде неполных приведенных затрат:

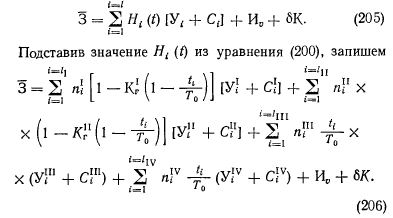
Выражение (206) справедливо для случая, когда ущербы при отказе любого элемента системы одинаковы. Возможен случай, когда даже в однородной системе (состоящей из одинаковых, равнонадежных элементов) их отказ приводит к различным ущербам. Тогда

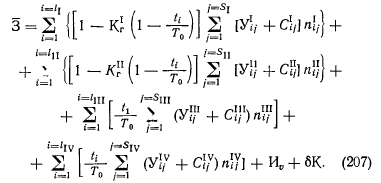
Очевидно, для неоднородного узла или системы выражение (207) усложняется за счет введения различных значений Т0 в соответствующих точках фазового пространства.

Ущерб при отказе системы определяется недоотпуском электроэнергии от ТЭЦ и связанным с этим перерасходом топлива в комплексе ТЭЦ — энергосистема:

Рассмотрим переменные первой группы. Текущее время — независимая переменная, принимающая детерминированные значения, соответствующие длительности расчетных режимов или их отрезков в течение расчетного периода. Снижение мощности при отказе AN{ — зависимая переменная, являющаяся в условиях локальной задачи функцией независимой переменной:

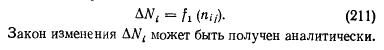
Закон изменения ANt может быть получен аналитически.

Перерасход топлива за счет вовлечения системы ДЬ — независимая переменная, изменяющаяся в заданном диапазоне:

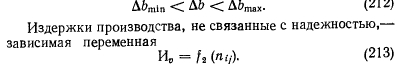
Закон изменения И0 может быть задан в детерминированной табличной форме.

Полная стоимость восстанавливаемого агрегата К — независимая переменная. В общем случае К является нелинейной функцией производительности и параметров агрегата (элемента схемы). Однако при точном сметном расчете может приниматься детерминировано в табличной форме. Стоимость замыкающего топлива — независимая переменная, изменяющаяся в заданном диапазоне

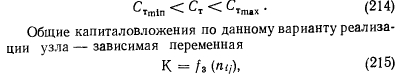
Рассмотрим переменные второй группы. Эти величины заданы в неопределенной форме с неизвестным законом распределения. С определенностью можно указать только достаточно широкий диапазон их изменения и средние базисные значения:

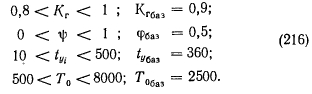
Методом оптимизации, наиболее соответствующим структуре функций цели и особенностям переменных, является перебор на сетке. Значение шага сетки может быть выбрано на основании следующих соображений. По характеру элементов, входящих в узлы, последние могут быть разделены на три большие группы: энергетические, структурные, комбинированные.

Энергетические узлы состоят из элементов, потребляющих или преобразовывающих энергию (например, котлоагрегаты, питательные насосы, бойлера). Для этих узлов шаг сетки определяется дискретным рядом серийно выпускаемых элементов. Структурные узлы состоят из элементов, регулирующих распределение энергетических потоков (арматура, регуляторы). Для этих узлов шаг сетки выбирается произвольно, с учетом требований действующих норм и условий эксплуатации. Комбинированные узлы состоят из элементов первой и второй групп. Таким образом, значения функции цели в узлах сетки могут быть реализованы с помощью ЭВМ с последующим выбором минимального значения.

Дальнейшее построение модели целесообразно разбить на три этапа.

На первом этапе полагаем переменными только величины t, ДN, tii, Hv, остальным придаем постоянные базисные значения. Минимизация функции цели (например, выражения (210)) по указанным переменным методом перебора на сетке дает искомый результат при введении линейных ограничений. Этот результат может быть выражен определенным приоритетным номером (рангом) варианта с меньшими приведенными затратами перед вариантом с большими затратами. Весь ряд значений приведенных затрат имеет вид

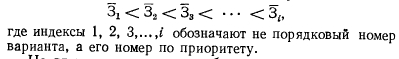
На втором этапе нарушим базисные значения величин Кг, Т0, /у., ф, К и, учитывая диапазон их задания, определим влияние этих переменных на структуру ряда. Для этого, приняв крайние значения интервала изменения для каждой из вышеуказанных величин, определим значения функции цели в этих точках для всех вариантов значений nif. Те переменные, значения которых не меняют приоритетного номера варианта (не влияют на его устойчивость и при переходе к третьему этапу оптимизации), могут учитываться как постоянные величины по их базисным значениям.

На третьем этапе необходимо учесть влияние величин, заданных в неопределенной форме, на значение функции цели. Диапазон значений неопределенных величин определяют зоны получаемых значений расчетных затрат при учете неопределенности. Изменение самой величины в указанном диапазоне берется с произвольным, желательно минимальным, шагом. Подобная операция выполняется для каждого рассматриваемого варианта задачи. Сущность вопроса можжет быть сформулирована так. Необходимо сделать выбор из множества предполагаемых оптимальных решений Alt А2,..., Ат, имея в виду, что предпочтительность каждого решения зависит от того, какое из сочетаний случайных величин ?1, ?2,..., 1 „ для него существует. Для условий нашей функции цели, если учитывать влияние неопределенности только одной величины, скажем Г0, решение вопроса формально изображается прямоугольной матрицей:

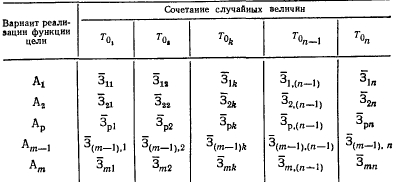
При наличии в функции цели нескольких неопределенных величин задача значительно усложняется, так как порядок матрицы возрастает соответственно их количеству. В данном случае необходимо было бы рассматривать матрицу третьего порядка для получения всей области значений неполных расчетных затрат с учетом неопределенности исходной информации. Расчет такой матрицы может быть реализован с помощью релаксационного метода, полагая поочередно изменяющейся одну из неопределенных величин при постоянстве остальных.

Может быть и несколько иной подход к определению области возможных значений функции цели. Определяют величины функции цели только для крайних значений диапазона изменения неопределенных величин, что приводит к сокращению количества столбцов в полной матрице. Для анализа полученной области возможных оптимальных значений и выбора окончательного решения при анализе матрицы могут быть применены специальные критерии теории игр.

Выбираем решение, имеющее наименьшее значение показателя Зр.

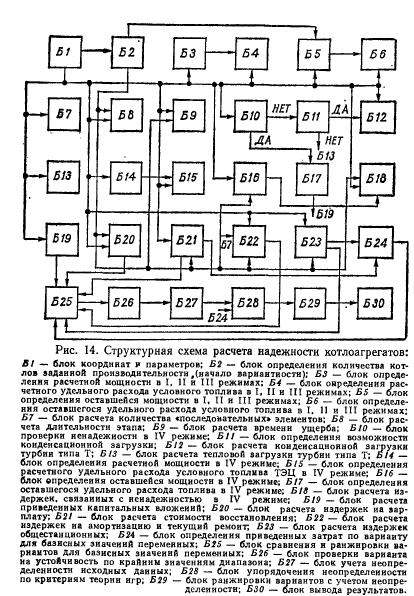
В том случае, если решения по всем критериям совпадают, задачу можно считать решенной. Если решения не совпадают, необходимо сужать диапазоны значений неопределенных величин, определяя для них новое значение диапазона, удовлетворяющее всем критериям. При необходимости расчета с помощью ЭВМ на рис. 14 изображена структурная схема программы.

Виноградов Ю. И., Векштейн Л. М., Соболь И. Д. ПРОМЫШЛЕННОЕ ТЕПЛОСНАБЖЕНИЕ. «Техника», 1975