КОМПЛЕКС ПРОГРАММНЫХ СРЕДСТВ ДЛЯ АНАЛИЗА НОВЫХ РЕСУРСОСБЕРЕГАЮЩИХ И ЭКОЛОГИЧЕСКИ ЧИСТЫХ ПРОЦЕССОВ ПРОКАТКИ
Для определения основных параметров технологических процессов горячей и холодной прокатки, в том числе асимметричных, разработан пакет прикладных программ работы с ПЭВМ. В основу пакета положена обобщенная математическая модель очага деформации при прокатке с использованием метода конечных элементов.Разработан ряд новых технологических процессов прокатки, в частности несимметричная холодная прокатка полос, прокатка труд нодеформируемых металлов в многовалковых калибрах, шаговая прокатка, в том числе полых профилей. Использование этих процессов позволяет повысить точность геометрических размеров изделий, интенсифицировать производство сплошных и полых профилей, снизить потери металла в угар, уменьшить шум и вибрацию при работе прокатного оборудования. Для использования этих преимуществ необходимо оптимизировать основные параметры технологических процессов.
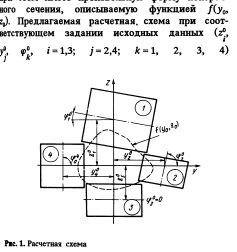
Расчетная схема для построения математической модели очага деформации выбиралась с учетом анализа максимально возможного числа вариантов процесса прокатки. В качестве базы выбрана схема очага деформации при прокатке в четырехвалковом калибре с гладкой бочкой при наклоне рабочих валков под произвольными углами (рис. 1). Заготовка при этом имеет произвольную форму поперечного сечения, описываемую функцией f(y09 z0). Предлагаемая расчетная, схема при соответствующем задании исходных данных может быть трансформирована в известные схемы процесса прокатки в двух, трех или четырехвалковых калибрах. Кроме того, расчетная схема (см. рис. 1) может быть сведена к нетрадиционной схеме процесса прокатки, что позволяет проектировать также и новые технологические процессы прокатки.
Для единой математической модели анализа процессов горячей, теплой и холодной прокатки необходимо иметь определяющие уравнения характеристик механических свойств прокатываемого материала, справедливые для всего температурноскоростного интервала процессов прокатки. Такое уравнение получено на основе анализа соотношения скоростей упрочнения и разупрочнения металла в процессе прокатки. Оно * представляет собой функционал сопротивления металла пластической деформации: где t — момент времени, для которого выполняется расчет; б (в0)— сопротивление ме 5о талла пластической деформации в исходном состоянии, зависящее от начальной температуры металла 0О; а, п— коэффициенты кривой упрочнения; А(т)— функция закона изменения во времени степени деформации сдвига; Я(т) — функция закона изменения во времени интенсивности скоростей деформаций сдвига; к(в) — коэффициент, характеризующий разупрочнение металла во время паузы, зависящий в общем случае от температуры 0.
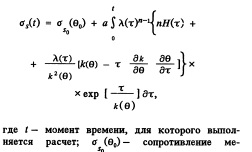
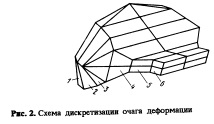
Для анализа эффективности различных процессов прокатки необходимо знать напряжен нодеформированное состояние металла в очаге деформации. В качестве основного алгоритма для его определения выбран алгоритм метода конечных элементов. При этом стремились ограничиться невысокими степенями полиномов и удовлетворить максимально возможное число накладываемых ограничений. Получили пробные функции с максимальным числом коэффициентов, равным 7, удовлетворяющих условиям несжимаемости, кинематическим соотношениям, дифференциальным уравнениям равновесия и физическим уравнениям связи касательных напряжений и сдвиговых деформаций. При этом очаг деформации разбивается на конечные элементы, имеющие вид треугольных призм и тетраэдров с семью узлами. При дискретизации очаг деформации условно разбивается на зоны: неравномерного (1) и равномерного (2) по ширине обжатий горизонтальными валками; неравномерного (3) и равномерного (4) по высоте обжатий упругого сплющивания горизонтальных (5) и вертикальных (б) валков (см. рис. 2).
Для преобразования краевой задачи к системе линейных уравнений применен метод Га леркина с линеаризацией определяющих соотношений. Система линейных уравнений решается методом Гаусса.
Пакет прикладных программ включает в себя расчетные модули и "дружественный" интерфейс. Расчетные модули реализуют обобщенную математическую модель очага деформации и включают в себя программы дискретизации, вычисления сопротивления металла пластической деформации, решения систем линейных уравнений и т.п.
Разработанный комплекс программных средств позволяет на основе математической модели определять напряженно
деформированное состояние очага деформации в известных и нетрадиционных процессах прокатки для оптимизации условий осуществления прогрессивных технологических процессов обработки черных металлов, проектирования новых процессов и оценки их эффективности.
СБОРНИК НАУЧНЫХ ТРУДОВ Черная металлургия России и стран СНГ в XXI веке. Т о м I, Москва 1994
