Определение неравномерности потребности в регулирующем объеме бака водоподогревателя в период определенной интенсивности потребления (ПОИП)
В этой части будет определена связь между расходом наполнения и регулирующим объемом бака за период определенной интенсивности потребления в зависимости от вероятности появления потребности в этом объеме. Схема системы наполнения представлена на рис. 3.2.
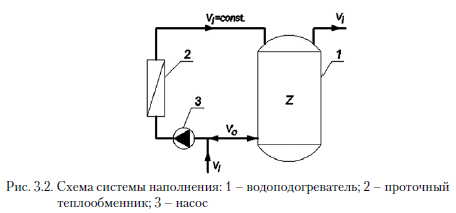
Переменная, определяющая расход воды, вытекающей из водоподогревателя - это разница двух параметров: расхода отбора и расхода подпитки. Считается, что подпитка происходит постоянно и что подпитывающий расход постоянен. Принимается также, что в этот период процесс открытия водоразборной арматуры можно описать с помощью процесса Пуассона с постоянной и известной интенсивностью. Распределение изменения отборов горячей воды при одном открытии водоразборного крана описывается как экспоненциальное распределение с известным параметром.
Объем бака определяют для времени максимальной интенсивности отбора. Считается, что по отношению к отрезкам времени между моментами отбора воды длительность максимального отбора настолько велика, что в аналитических рассуждениях можно считать ее неограниченной. Такое решение возможно тогда, когда среднее поступление тепловой энергии или воды в бак больше среднего отбора. Эту проблему можно разрешить несколькими способами [5; 30; 31; 40]. Рассмотрим один из них - определение максимума случайного блуждания так называемым способом «ступенчатых точек» [30].
Работу системы подпитки можно представить в виде стохастического процесса, связанного со случайным блужданием. Для упрощения отборы V[ приписываются, как и ранее, определенным моментам. Рассматривается состояние, имеющее место в момент отбора. Количество поступающей между отборами воды из теплообменника в бак пропорционально разнице времени между последним и текущим отбором. Если промежуток времени между последним и происходящим отбором i обозначим Дт, то поступающей объем воды в это время составляет:
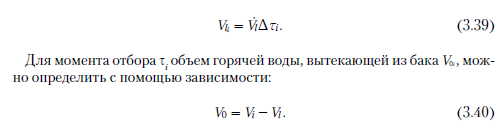
Способ определения последующих объемов горячей воды, вытекающих из бака, представлен на рис. 3.3.
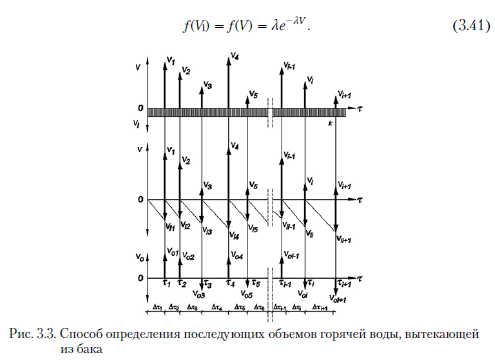
Потребление горячей воды 14 и объем горячей воды Vu, подпитывающей бак в определенный момент, являются случайными переменными. Следует определить распределение случайной переменной 14, описывающей изменение объема воды, поступающего из бака, который является разницей этих случайных переменных. Случайную переменную 14, определяющую отбор горячей воды при одном открытии водоразборного крана, можно описать с помощью экспоненциального распределения, общего для всех отборов. Плотность распределения определяют зависимостью:
Случайная переменная Voiy определяющая объем воды, подпитывающей бак, является произведением постоянного параметра (расхода подпитки) и случайной переменной Дт, соответствующей длительности времени между отборами. Случайная переменная Дт; обладает экспоненциальным распределением, что является результатом свойств процесса Пуассона с постоянной интенсивностью. Если случайную переменную с данным распределением умножить на постоянную величину, то вид распределения новой переменной такой же, как и старой [5]. Плотность распределения длительности между следующими моментами, приписанными отборам, определена как общая зависимость для всех отрезков времени Дту
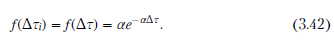
В то же время плотность распределения, определяющего объем воды, поступающей в бак (питающей бак) между отрезками, соответствующими отборам, описывают формулой:
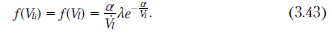
Ищем распределение случайной переменной, которая является разницей двух переменных с экспоненциальным распределением:
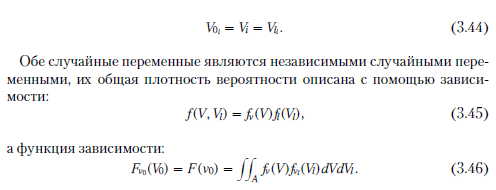
Случайные переменные V и И/ могут принимать положительные значения, в то время, как переменная У0, определенная зависимостью (3.44), может принимать как положительные, так и отрицательные значения. Площадь существования переменной V0 вместе с пределами и разбиением на площади интегрирования представлена на рис. 3.4.
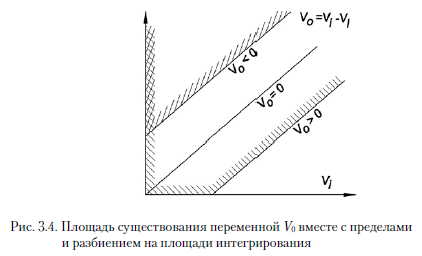
Ввиду различного определения пределов площади существования случайной переменной для положительных и отрицательных значений для этих значений функция распределения определена отдельно, на основании зависимости (3.46):
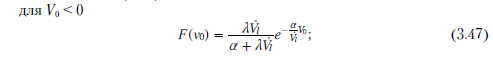
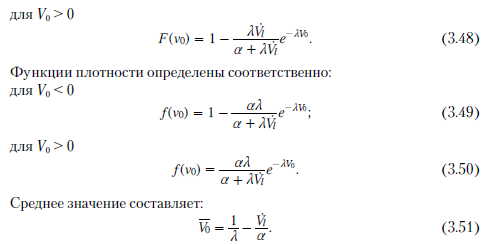
Значения VohVo2...Voi являются случайными переменными с общим распределением, определенным функцией распределения F. Искомым является распределение максимумов следующих сумм вышепредставленных случайных переменных. Таким образом, рассматривается последовательность случайных переменных:
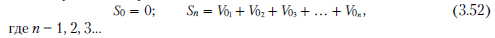
Предположим, что имеем дело с процессом, в котором Дть Дт2, Дт3... Дт„ являются моментами появления сигналов, 5) - это величина сигнала в момент Ti; V, - прирост папраметра. В начальный момент сигнал не появляется. Считается, что в и-ную минуту произошла рекордная величина сигнала, если:
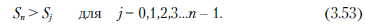
Это значит, что в момент т„ значение сигнала положительно и больше значений во всех предыдущих моментах. Показатель п, для которого неравенство (3.53) появилось первый раз, называется первым показателем ступени. Это показатель, для которого Sn первый раз стал положительным, (в начальный момент S0 = 0 по принципу: последующие приросты V), могут быть положительными или отрицательными: так, что первое положительное значение может появиться спустя длительный период времени или же вообще не появиться). Показатель п, для которого неравенство (3.53) имеет место к раз, называется к-ступенчатым параметром. Величина сигнала описывается как к-ступенчатая величина. Считается, что в распределении, определенном функцией распределения F, существует ограниченная ожидаемая величина р. Если р > 0, то ступенчатые параметры имеют тенденцию к неограниченному уменьшению. Ступенчатых точек вообще может не быть либо может быть их ограниченное количество, а потому будет существовать максимальная ступенчатая точка, т. е. максимальное значение во всем процессе. Если р = 0, то процесс является осциллирующим.
Доказано, когда существует только предельное количество ступенчатых точек, то последняя (и-ная) - экстремальная и распределение ее величины описано и-ной композицией распределения величины первой ступенчатой точки [5].
Шафлик В./Современные системы горячего водоснабжения. - К.: ДП ИПЦ «Taici справи», 2010.
