АНАЛИЗ И ОБСУЖДЕНИЕ КОЭФФИЦИЕНТ ТЕПЛООТДАЧИ
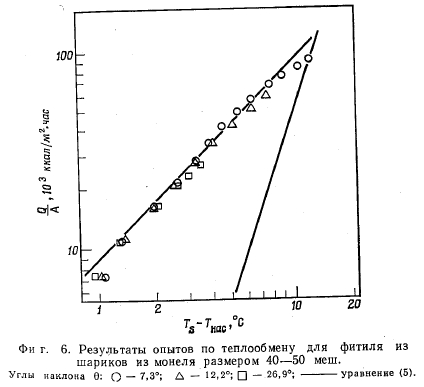
На фиг. 6 показаны данные трех опытов, проведенных с использованием шариков из монеля размером 40— 50 меш для трех различных углов наклона О тепловой трубы с регулируемыми условиями окружающей среды. Эти данные относятся к области ниже критического теплового потока и описываются прямой с наклоном, равным единице, что указывает на постоянство коэффициента теплоотдачи. Для сравнения приведены данные Феррелла и Олливитча [5], полученные при кипении в большом объеме на поверхности из нержавеющей стали, имеющей одинаковую чистоту поверхности.
Среднее значение коэффициента теплоотдачи можно определить из следующего соотношения:
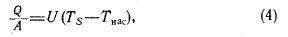
которое на фиг. 6 описывается прямой с наклоном, равным 1.
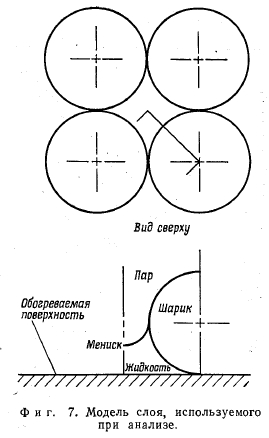
Объяснение опытных данных можно получить на основе анализа последовательности процессов, происходящих по мере возрастания теплового потока на поверхности. Последующее обсуждение и модель (фиг. 7) основаны на рассмотрении процесса переноса тепла в слое, образованном сферическими шариками. При увеличении теплового потока жидкость и шарики, находящиеся в контакте с поверхностью, постепенно перегреваются, т. е. приобретают температуру, превышающую температуру насыщения системы. В конце концов перегрев слоя, состоящего из жидкости и шариков, у поверхности нагрева возрастает настолько, что образуется граница раздела жидкость — пар. Наиболее вероятным местом образования такой границы раздела фаз является область минимального диаметра поры, образованной слоем шариков, находящихся в контакте с поверхностью. Тепловой поток от поверхности проходит через слой шарики — жидкость к границе раздела фаз, расположенной у минимального диаметра поры в первом слое шариков. Движение жидкости сквозь небольшие поры в слое шариков носит ламинарный характер в отличие от турбулентного конвективного течения, возникающего вследствие отрыва пузырей пара при кипении жидкости в большом объеме.
В результате сопротивления при течении через пористый материал на обогреваемой поверхности образуется относительно неподвижный слой жидкости. Этот слой непрерывно пополняется за счет подсасывающего эффекта, вызываемого действием капиллярных сил, компенсируя потерю жидкости при испарении.
В работе Чэнга [3] показано, что действие капиллярных сил не зависит от интенсивного испарения жидкости на границе раздела фаз жидкость — пар, поэтому движущий напор можно рассчитать на основе экспериментальных данных по подъему жидкости в капилляре с учетом влияния изменения температуры на поверхностное натяжение и плотность.
Механизм образования границы раздела жидкость — пар в слое шариков, находящихся в контакте с поверхностью, неизвестен. Граница раздела фаз может возникать в процессе парообразования на обогреваемой поверхности или на поверхности шариков или может образовываться вблизи вершины фитиля и затем перемещаться к своему окончательному положению. В любом случае из опытов следует, что положение границы раздела фаз, коль скоро она локализовалась, остается фиксированным вплоть до возникновения критического теплового потока. Кроме того, полученные данные свидетельствуют о полном отсутствии процессов, которые являются определяющими при пузырьковом кипении жидкости в большом объеме. При пузырьковом кипении число активных центров парообразования существенно зависит от температуры поверхности, поэтому коэффициент теплоотдачи зависит от температуры поверхности или теплового потока. Полученные в опытах данные со всей очевидностью свидетельствуют об отсутствии такой зависимости. Однако попытка проверить эти выводы с помощью визуальных наблюдений через стеклянную часть тепловой трубы оказалась безуспешной.
На основе предложенного механизма процесса теплообмена была решена численными методами трехмерная стационарная задача теплопроводности для двух областей: жидкой и твердой (шарики). Модель кубической единичной ячейки и положение границы раздела фаз жидкость — пар показаны на фиг. 7. Задавались следующие граничные условия: температура поверхности стенки принималась постоянной, температура на границе раздела фаз жидкость — пар равна температуре насыщения, а значения температур и тепловые потоки непрерывны на границах областей. Величина контактного термического сопротивления между шариками и поверхностью определялась экспериментально путем изменения площади контакта каждого шарика с поверхностью при условии идеального контакта этой площади (табл. 2). Подробное описание уравнений и особенностей численного метода можно найти в работе [6].
Результат расчета среднего значения коэффициента теплоотдачи при условии точечного контакта между частицами и поверхностью и осреднения двух исследованных форм менисков для шариков из монеля сводится к уравнению
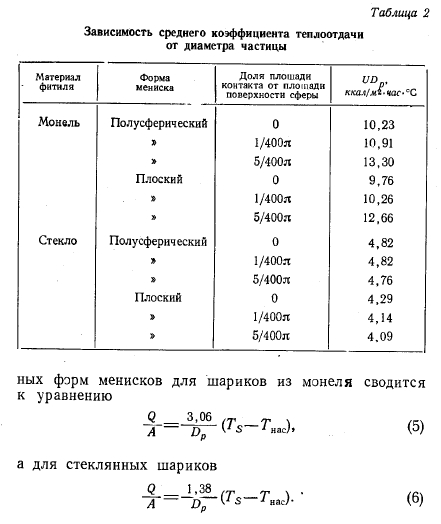
Влияние контакта шарик — поверхность и фермы мениска на коэффициент теплоотдачи на основе результатов расчета показано в табл. 1.
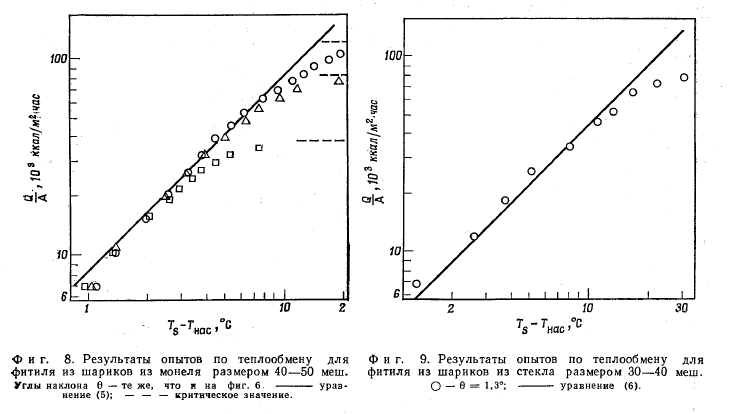
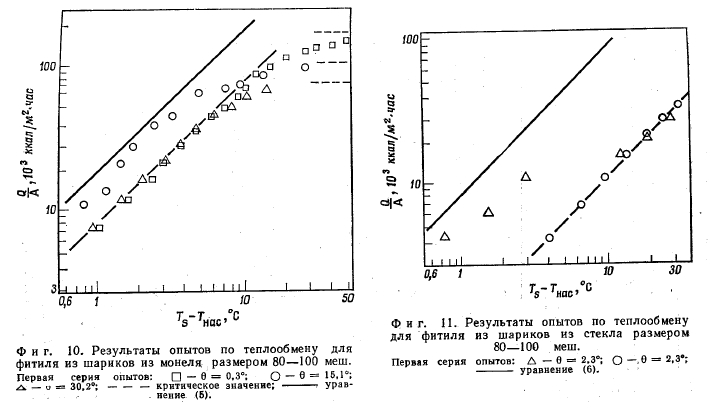
Полностью данные для шариков из монеля размером 40 50 меш и из стекла размером 30—40 меш приведены на фиг. 8 и 9. Экспериментальные данные хорошо согласуются с расчетными в области тепловых потоков ниже критического. Для частиц наименьшего размера (80— 100 меш) наблюдается худшее совпадение. Результаты такого сопоставления приведены на фиг. 10 и 11. В обоих случаях данные первого опыта хорошо согласуются с результатами теоретического расчета, а затем наблюдается значительнее расхождение. После первоначального смещения опытные течки последующих опытов ложатся на одну и ту же прямую.
Как видно из фиг. 10 и 11, хотя опытные данные и не согласуются с расчетными значениями, они хорошо описываются прямой с наклоном, равным единице, что свидетельствует о постоянстве коэффициента теплоотдачи и справедливости предложенного механизма теплообмена. Наиболее вероятное объяснение такого расхождения заключается в том, что граница раздела жидкость — пар находится не в первом слое шариков, а в слое, расположенном дальше от поверхности, что приводит к уменьшению коэффициента теплоотдачи.
При осмотре этих слоев шариков после проведения опытов были обнаружены загрязнения вблизи поверхности нагрева, которые могли оказать определенное влияние на результаты, однако причина образования этих загрязнений в настоящее время неизвестна.
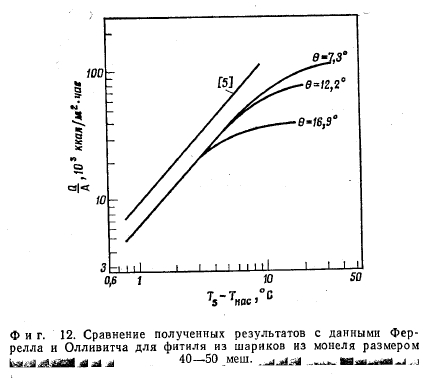
Сравнение данных, представленных на фиг. 8, с данными Феррелла и Олливитча [5] для шариков из монеля размером 40—50 меш приведено на фиг. 12. Даже в этих двух различных установках, на которых были получены опытные данные, механизм процесса, по-видимому, был одинаковым. Расхождение в количественных результатах опытов можно объяснить разной степенью воздействия, которое оказывает удерживающая сетка в этих двух различных конфигурациях тепловой трубы, что проявляется в степени контакта между частицами и поверхностью. Влияние контакта на коэффициент теплоотдачи показано в табл. 2. Характер контакта между фитилем и обогреваемой поверхностью вносит основную неопределенность при расчете величины коэффициента теплоотдачи.
КРИТИЧЕСКИЙ ТЕПЛОВОЙ ПОТОК
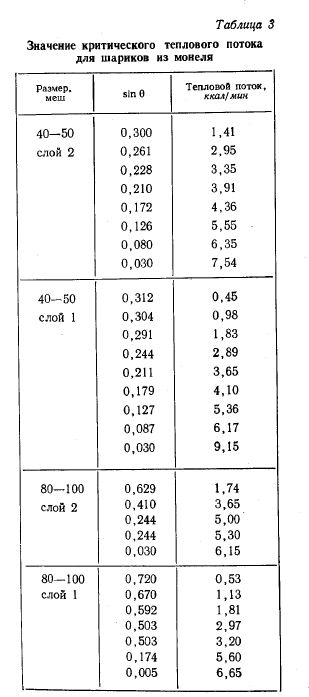
Как видно из данных, представленных на фиг. 8—10, при достижении критического теплового потока температура поверхности возрастает, что приводит к отклонению экспериментальных точек от прямой. Вероятно, это происходит вследствие высыхания фитиля в области наибольшего эффективного диаметра поры. В этом случае кризис определялся по полному высыханикГфитиля в его верхней части. Данные по критическим тепловым потокам представлены в табл. 3. Уравнение для расчета критического теплового потока было получено с помощью соответствующих уравнений сохранения массы, энергии и количества движения. В качестве критического теплового потока Q выбиралось такое значение теплового потока, при котором капиллярный напор уже не мог обеспечить необходимый поток жидкости против сил тяжести и силы трения жидкости и пара.
На основе рассмотренного механизма теплообмена было получено уравнение при условии, что пар движется по нормали от поверхности, а жидкость — параллельно поверхности. Площади поперечных сечений для каждого потока определялись в зависимости от поперечного сечения фитиля в направлении движения потока с учетом пористости для каждого потока. Сумма двух значений пористостей для потоков пара и жидкости равна общей пористости, определяемой обычным путем. Окончательное уравнение, выраженное через пористость для потока жидкости, имеет вид
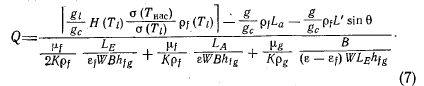
Подробный вывод этого уравнения дан в работе [6]. В уравнении (7) первый член в числителе представляет капиллярную движущую силу, зависящую от высоты равновесного капиллярного поднятия жидкости Я, как показано на фиг. 5. Индекс I относится к условиям измерения Я. Второй и третий члены учитывают влияние силы тяжести в тепловой трубе. Члены в знаменателе представляют собой соответственно трение жидкости в испарителе, трение жидкости в адиабатическом участке и трение пара в испарителе.
Проверка уравнения показывает, что критический поток Q является линейной функцией sin0, начальная ордината и наклон которой зависят от значения пористости Ё/ для потока жидкости. Кроме того, из уравнения видно, что при соответствующем выборе пористости для потока жидкости определяющим может стать либо член, учитывающий трение потока пара, либо трение потока жидкости. Поскольку теоретические или экспериментальные методы определения каждой из пористостей отсутствуют, теоретические кривые рассчитаны для различных значений обеих пористостей или поперечных сечений потоков.
На фиг. 13 экспериментальные результаты для шариков из монеля размером 40—50 меш сопоставлены с теоретическими кривыми. Кривая А рассчитана при таком значении пористости жидкости, при котором знаменатель уравнения (7) принимает минимальное значение, Что в свою очередь приводит к максимальным значениям начальной ординаты и угла наклона.
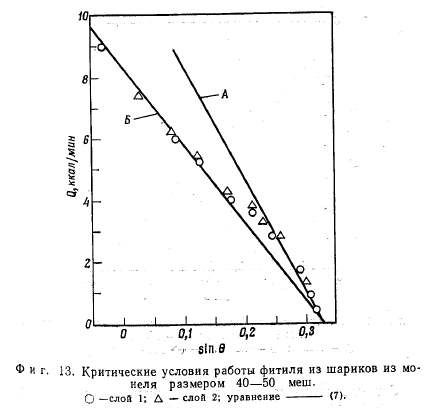
Кривая Б рассчитана для такого значения пористости жидкости, при котором значение знаменателя приблизильно в 1,5 раза больше его минимального значения с экспериментальными данными показывает что значение критического теплового ока нельзя точно рассчитать в широком диапазоне изменения угла наклоны с помощью одной кривой. Более того, это сравнение, по-видимому, говорит о том, что для[ точного расчета критического теплового потока необходимы отдельные соотношения, справедливые для различных значений sin0 во всем диапазоне его изменения.
Существование двух резко различающихся режимов работы тепловой трубы можно объяснить, учитывая, что i степень заполнения фитиля в испарительном участке зависит от угла наклона трубы.
Для больших углов наклона фитиль, по-видимому, не полностью наполняется (небольшие участки пор с большим эффективным диаметром не полностью пропитываются жидкостью). Следовательно, сила трения, обусловливающая движение пара через эти участки, будет меньше силы трения в случае, если пар и жидкость полностью взаимодействуют. Для малых углов наклона участки, не заполненные жидкостью, отсутствуют, что приводит к увеличению трения.
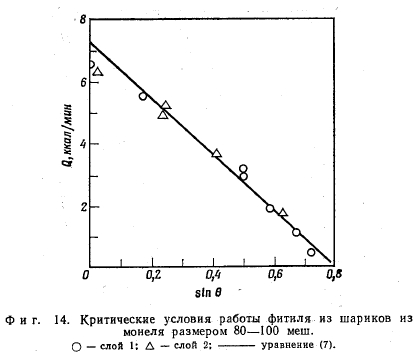
На фиг. 14 приведены результаты, полученные для шариков из монеля размером 80—100 меш. Расчетная кривая построена на основе тех же соображений, что и кривая А на фиг. 13.
В этом случае наблюдается хорошее совпадение расчетных и экспериментальных данных, однако почти все данные получены для больших углов наклона тепловой трубы и обнаруживают такой же характер зависимости, как и шарики размером 40—50 меш.
Причина, по которой на фиг. 13 использованы различные обозначения для двух различных слоев шариков, состоит в том, что для получения данных по критически тепловым потокам при различных углах наклона был использован специально подготовленный слой. Этот слой шариков был затем извлечен из тепловой трубы, шарики были тщательно очищены от загрязнений, и тепловая труба была вновь собрана из этих шариков. Хорошее совпадение данных, полученных для различных слоев шариков, показывает, что принятая методика заполнения шариками дает воспроизводимые результаты.
ВЫВОДЫ
Несмотря на некоторый разброс, все полученные данные подтверждают механизм процесса, предложенный во введении. Последующие исследования должны быть направлены на решение таких задач, как изучение течения жидкости и пара в пористых материалах, когда действие капиллярных сил является определяющим, изучение положения границы раздела фаз пар — жидкость в условиях испарения с обогреваемой поверхности и изучение влияния контакта между пористым материалом и обогреваемой поверхностью.
