ПЕРЕПАД ДАВЛЕНИЯ ПРИ ТЕЧЕНИИ ЖИДКОСТИ В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ
Градиент давления при течении электропроводной жидкости в однородном поперечном магнитном поле зависит от геометрии канала, отношения проводимостей стенки и жидкости С и числа Гартмана Н. Последние два важных безразмерных параметра определяются следующим образом:

Число Гартмана Н характеризует соотношение пондеромоторных и вязкостных сил в жидкости. Оно определяет интенсивность замкнутых токов в жидкости, индуцированных магнитным полем. При Н=0 мы имеем дело с обычным падением давления в вязкостном несжимаемом пограничном слое. С увеличением Н градиент давления возрастает, при этом, как будет показано в дальнейшем, градиент давления, является функцией как Н, так и С
В случае течения между параллельными пластинами имеется простое аналитическое выражение для градиента давления, справедливое для всех значений С и Н. Для других геометрий канала (в частности, для круглого и прямоугольного каналов) получены точные решения в виде бесконечных рядов. Однако эти выражения очень громоздки. К счастью, градиент давления в этих каналах может быть достаточно точно аппроксимирован простой эмпирической формулой, полученной на основе решения для случая течения между параллельными пластинами.
Выражение для градиента давления при полностью развитом ламинарном течении несжимаемой жидкости между параллельными пластинами и при наличии однородного поперечного магнитного поля было получено в работе. Это выражение может быть записано следующим образом:

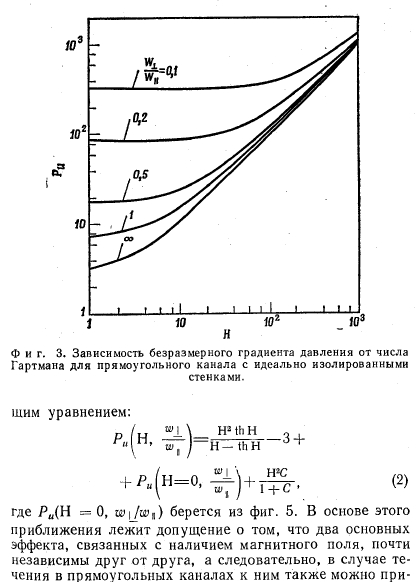
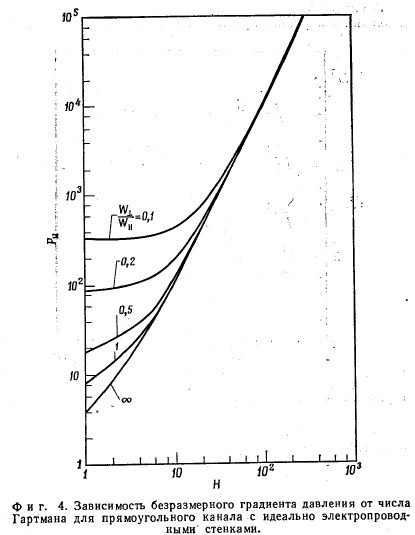
В работах [4,5] были получены соотношения для градиента давления при полностью развитом ламинарном течении несжимаемой жидкости в прямоугольном канале при наличии однородного поперечного магнитного поля для двух предельных случаев С = 0 и С =оо. В обоих случаях решение получается в виде бесконечного ряда. На фиг. 3 представлены результаты расчетов с помощью этих рядов для случая С = 0, а на фиг. 4, представляющий собой отношение полуширины канала в направлении, перпендикулярном магнитному полю, к полуширине канала в направлении, параллельном магнитному полю. На обоих графиках показаны кривые, соответствующие случаю течения между плоскими параллельными пластинами (w±/w\i = оо).
В случае течения в прямоугольном канале градиент давления с хорошим приближением описывается следую-
Для того чтобы получить достаточно точные результаты при Н-0 для прямоугольных каналов, уравнение
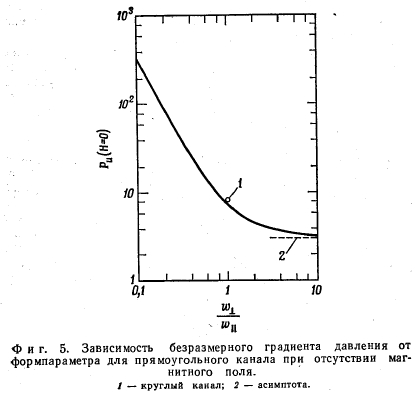
Это эмпирическое уравнение является точным и при очень больших значениях Н и дает незначительные ошибки при промежуточных значениях Н. Например, при С = 0 и при значениях формпараметра больше 0,1 ошибка в определении Ри никогда не превышает 11%. При С =оо ошибка почти на порядок меньше. При значениях С, лежащих между 0 и оо,-точные решения отсутствуют. Однако представляется достаточно обоснованным допущение о том, что в этом случае погрешность расчета по приближенной формуле будет меньше погрешности определения Ри при С = 0.
Уравнение (2) также дает хорошее приближение и для градиента давления в круглом канале [в этом случае Ри(Н =0) =8,0]. Точное решение, представляющее собой бесконечный ряд функций Бесселя, было выведено Ихара [6]. Расчет с помощью приведенного в работе аналитического выражения не повторялся; при сравнении точного и приближенного решений пользовались данными, взятыми из графиков, приведенных в этой же работе. Было найдено, что максимальная ошибка расчетов по нашей приближенной формуле составляет менее 10%.
Ряд эффектов, таких, как шероховатость стенки, подвод и отвод массы к рассматриваемому потоку, не учитываются уравнением (2). В реальной тепловой трубе рабочая жидкость обычно течет по замкнутым каналам с негладкими стенками. В тепловой трубе типа I капиллярные поры могут в отдельных местах соединяться между собой. В тепловой трубе типа II каналы для протока жидкости с одной стороны прикрыты мелкой сеткой или проницаемым экраном. Шероховатость стенки прежде всего скажется на величине члена Ри (Н =0, W\/Wt)в уравнении (2).
Влияние подвода или отвода массы к потоку жидкости будет мало, если выполняется условие
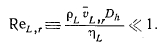
В тепловой трубе типа I это условие почти всегда удовлетворяется, поскольку гидравлический диаметр капилляров очень мал. В тепловой трубе типа II, специально спроектированной для работы в сильном поперечном магнитном поле, гидравлический диаметр канала для жидкости, а тем самым и число Рейнольдса радиального потока будут значительно больше. Следовательно, вблизи пористой стенки канала существенную роль будут играть как вязкостные, так и инерционные эффекты. Для количественной оценки степени влияния инерционных сил необходимы дальнейшие аналитические исследования; безусловно, необходима также надлежащая экспериментальная проверка полученных результатов.
Для того чтобы в канале для жидкости преобладал вязкостный режим течения, в дополнение к указанному выше требованию должно выполняться следующее условие: осевое число Рейнольдса повсюду должно быть значительно больше радиального. Эго условие в типичных конструкциях тепловых труб повсюду легко соблюдается, за исключением самых крайних участков трубы, где осевая скорость стремится к нулю.
Таким образом, можно сказать, что уравнение (2) представляет собой очень хорошее приближенное аналитическое выражение для расчета перепада давлений в электропроводных жидкостях, текущих в замкнутых каналах с электропроводными стенками при наличии однородного поперечного магнитного поля. Единственным ограничением служит требование, чтобы течение было полностью развитым, ламинарным и несжимаемым. Это условие почти всегда удовлетворяется при течении жидкости в тепловых трубах типа I, поскольку значения осевых чисел Рейнольдса в них меньше 2300, т. е. меньше критического числа Рейнольдса. Кроме того, очень большая величина отношения длины трубы к диаметру обеспечивает условия, при которых можно пренебречь влиянием начального участка. В тепловой трубе типа II гидравлический диаметр канала для прохода жидкости увеличивается настолько, что указанные выше условия уже могут быть нарушены по крайней мере в случае отсутствия магнитного поля. Однако наложение сильного поперечного магнитного поля ведет как к увеличению критического числа Рейнольдса [7], так и к уменьшению длины начального участка [81, так что допущение о существовании полностью развитого ламинарного течения может все еще оказаться справедливым. Мы будем считать, что уравнение (2) применимо для обоих типов тепловых труб как при наличии, так и при отсутствии магнитных полей.
