МЕТОДИКА ОПРЕДЕЛЕНИЯ ПРОФИЛЯ ИНСТРУМЕНТА ДЛЯ ОБРАБОТКИ РАБОЧИХ ПОВЕРХНОСТЕЙ РОТОРОВ ВИНТОВОГО КОМПРЕССОРА
Одним из факторов, определяющих энергетические показатели винтового компрессора, является точность изготовления винтовых профильных поверхностей роторов, образующих рабочую полость.
Решение вопросов точности изготовления спрофилированных винтовых поверхностей роторов винтового компрессора невозможно без наличия точной методики расчета образующей режущего зуба фрезы, формирующие в процессе обработки профильные поверхности.
Существует несколько методов решения данной задачи [1 - 5], каждая из них имеет свои преимущества и недостатки. Остановимся более подробно на анализе метода предложенного П.А. Андреевым [1], так как именно в этом методе наиболее полно отражены основные подходы расчета инструментов дискового типа, применяемых на протяжении ряда лет при производстве роторов винтовых компрессоров.
Исходными, для определения профиля режущего зуба фрезы в этом методе, являются уравнения участков кривых, формирующих профиль ротора в торцевом сечении (рис. 1), что ставит решение задачи в зависимость от этих параметрических уравнений.
На рисунке 1 точки A1, B1, C1, D1, F1, E1 - границы участков образующих профиль ротора винтового компрессора в торцевом сечении и соответствующие точки профиля режущего зуба фрезы.
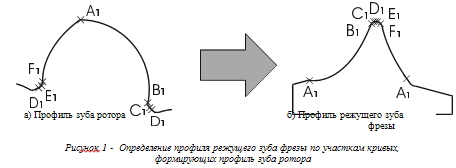
При таком подходе, для определения профиля режущего зуба фрезы конкретного винтового профиля ротора, необходимо иметь отдельную расчетную программу. А корректировка программы, при изменении профиля винта ротора, как правило, требует трудоемких математических преобразований, с использованием сложных исходных параметрических уравнений и переработки расчетной программы в целом.
Альтернативой такому “негибкому” расчету инструментальной поверхности предлагается методика расчета профиля режущего зуба фрезы исходя из массива координат профиля ротора (рис. 2), не привязываясь к его конкретным параметрическим уравнениям.
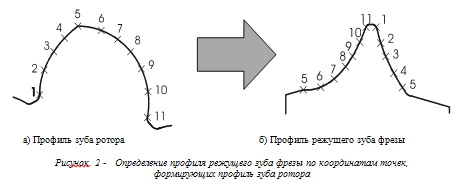
Суть метода состоит в том, что торцевое сечение профиля винтового ротора задается массивом координат (рис. 2а), который затем аппроксимируется участками прямых, проведенных через две соседние точки, а расчет профиля режущего зуба инструмента сводится к нахождению на профиле режущего зуба фрезы соответствующей образующей точки (рис. 2б).
Ниже рассматривается аналитический метод расчета профиля зуба режущей фрезы для обработки винтовой поверхности ротора винтового компрессора.
Закрепив ось фрезы, и обкатывая вокруг этой оси обработанную поверхность, получим семейство поверхностей в пространстве. Поверхность вращения, изнутри огибающая все это семейство поверхностей, является профилем режущего зуба фрезы (без учета стружечных канавок).
В процессе чистовой операции профиль режущего зуба фрезы касается винтовой поверхности ротора по некоторой линии резания, которая, будучи линией соприкосновения огибающей с одной из поверхностей семейства, является, характеристикой этой поверхности. Таким образом, расчет профиля режущего зуба фрезы сводится к нахождению одной характеристики описанного выше семейства поверхностей. Вся режущая поверхность фрезы описывается вращением этой линии вокруг оси фрезы.
Для аналитического расчета профиля режущего зуба фрезы приняты следующие обозначения:
Связь между координатами изделия x, y, z и инструмента xф, yф, zф выражается следующей системой уравнений преобразования координат:
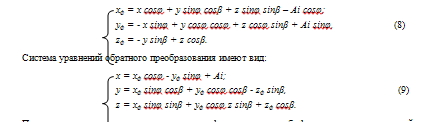
Примем некоторую точку на поверхности профиля режущего зуба фрезы, лежащую в данный момент на линии резания. Координаты точки xф , yф, zф в системе координат, связанной с фрезой, очевидно, не меняются при вращении последней. Вращению фрезы соответствует изменение угла . Положение же данной точки в пространстве изменяется, оно характеризуется координатами этой точки x, y, z в системе, не связанной с фрезой. Бесконечно малое перемещение точки в пространстве характеризуется дифференциалами координат x, y, z при бесконечно малом изменении угла . Величину перемещения точки получим дифференцируя (9) по углу :


Решение трансцендентного уравнения заданного координатой точки профиля ротора винтового компрессора позволяет найти образующую точку на профиле режущего зуба фрезы. Задаваясь рядом значений параметра t, методом последовательных приближений находится единственно верное решение, удовлетворяющее уравнению (20).
Координаты x, y, z заданной точки профиля ротора, которая принадлежит линии резания, определяется из уравнения винтовой поверхности (18) с использованием полученных величин.
Образующая координата точки профиля режущего зуба фрезы Rф и Zф определятся путем перехода из систем координат изделия (ротора) в систему координат инструмента (фрезы) при помощи выражений:
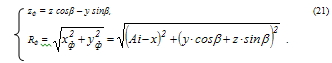
Сравнительные исследования, проведенные с целью сопоставление координат фрезы, рассчитанных по предлагаемому методу, с результатами расчета по программе, разработанной на основе параметрических уравнений участков кривых, формирующих профиль ротора, показали, что расхождения расчета возникает лишь в сотых долях микрона.
Для наглядности в таблице 1 представлены результаты расчетов профиля режущего зуба фрезы по различным методикам в узловых точках профиля ротора (рис. 1).
Из таблицы 1 видно, что расхождения возникают только в пятом знаке после запятой.
Как показали проведенные исследования, точность расчета не зависит от дискретности заданного массива координат профиля зуба ротора.
Результаты практических исследований на различных массивах координат профиля зуба ротора позволяет сделать вывод о том, что разработанная методика расчета профиля режущего зуба фрезы, в отличие от имеющихся, является универсальной и может быть использована применительно к любой конструкции профиля различных винтовых поверхностей.
Кроме того, разработанная методика профилирования инструментальной поверхности применима для определения профиля, как дисковых фрез, так и абразивных кругов.
Труды XIII международной научно-технической конференции по компрессоростроению. Сумы 2004
