Земные навигационные системы координат

Для решения основной навигационной задачи прежде всего необходимо располагать информацией о координатах ВС и ОПМ в земной навигационной системе координат (СК), выбранной для выполнения полета. Указание положения объектов и точек на земной поверхности в зависимости от принятой формы Земли осуществляется в астрономической, геодезической и сферической системах координат. На практике широко пользуются термином географические координаты (широта ч>г и долгота Кг), хотя такой СК нет Под географической системой координат пони мают ортогональную сетку меридианов и параллелей на поверхности земного эллипсоида вращения, перенесенную на карту. Поэтому снятые с карты координаты точек называются географическими.

При решении многих задач воздушной навигации Землю принимают за сферу (шар) и пользуются нормальной сферической СК. Преобразование географических координат в нормальные сферические выполняют следующим образом:

Применение различных датчиков навигациониой информации, работа которых основана на самых разнообразных физических принципах, а также большое число навигационных задач, решаемых в процессе подготовки к полету и в по тете, обусловливают использование в воздушной навигации рачительного числа земных систем координат: географической, нормальной сферической, орто- тромнческой сферической, главной и частной ортотромической, плоской прямоугольной, полярной и биполярной, экваториальной, горизонтальной и др.

Для решения всех навигационных задач исходной информацией являются географические координаты, которые при необходимости прообраз} ютси в любые другие

Ортодромичсская сферическая СК (ОССК) представляет собой кос>ю сферическую систему, экватор кото рой располагается в любом требуемом направлении и называется главной ортодромией (условным экватором). Равноудаленные от нее две точки, в которых сходятся условные мерианы, принимаются за полюса Ро этой СК. Коор шпатами точки являются ортотромнческие широта и долгота: в градусной мере Z. X, в ли ней ной г, х Широта Z измеряется от плоскости условного экватора к полюсам системы от 0 до +90° Начало отсчета долготы А может быть выбрано произвольно, если оно не предопределяется особенностями бортового навигационного комплекса.

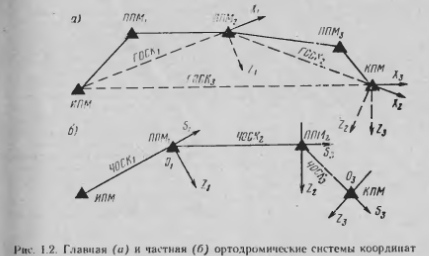
Если известны координаты точки вертекса «рг. Я,- ортодромии, то нормальные сферические координаты

В практике современной навигации условный экватор ОССК строится для всего мари оута (проходит через НПМ и КПМ). или нескольких участков, или каждого участка (рнс 1.2,а). В первом и втором случаях полученная СК называется главной ортодромической (ГОСК), в по еле тем — частной ортодромической (ЧОГК) В настоящее время наибольшее распространение получила ЧОСК. В ней начало СК выбирают в конце участка маршрута, ось OS совмещают с ортодромической ЛЗП участка (с условным экватором), а 01 (условный меридиан) направляют перпендикулярно оси OS (рис. I 2, б) Поскольку при полетах по воздушным трассам уклонения ВС от ЛЗП невелики, то в полосе маршрута поверхность Земли допустимо принимать за цилиндрическую. Тогда при развертке цилиндра получается практически плоская поверхность, а ЧОСК превращается в прямоугольную ортодромическую систему координат (ПОСК) Она может строиться непосредственно на полетной карте. Координаты 2, 5 ориентиров измерениями на карте будут определяться с методическими погрешностями, присущими этой СК- Их значения зависят от проекции и масштаба карты. Они равны нулю на ЛЗП и возрастают по мере удаления пунктов от оси OS. Хотя в полосе маршрута они несущественны, но тем не менее в современной воз 1ушной навигации коор шпаты пунктов рассчитываются с требуемой точностью по формулам сферической тригонометрии.

В прямоугольной ОСК земная поверхность считается плоской и задачи воздушной навигации решаются с использованием формул элементарной тригонометрии. Допустимость этого определяется теоремой Лежандра, согласно которой при выпрямлении сторон малого сферического треугольника каждый угол в полученном плоском треугольнике будет меньше соответствующего угла сферического треугольника на Ku—QIdRi, где Q — площадь треугольника. Если рассматривать равносторонний треугольник со сторонами, то справедливо соотношение 450 км и 900 км имеют место иска жеиня углов порядка Ли = 2,5 и 10 соответственно

Прямоугольная ОСК удобна дли контроля пути, навигационного управлении полетом и управления воздушным движением: координаты 2С и непосредственно указывают линейное боковое уклонение (ЛБУ) от ЛЗП и оставшееся до очередного ППМ расстояние. В этой СК упрощается и автоматизированное вождение ВС, так как для следования по лннин заданного пути.

Полярная и биполярная СК используются при эксплуатации радионавигационных систем, а экваториальная и горизонтальная — астрономических средств.

Воздушная навигация: справочник/А.М. Белкин. М.: Транспорт. 1988г.